AL SER.MO D. COSIMO MEDICI

PRINCIPE DI TOSCANA, ETC.

Se io volessi, Serenissimo Principe, spiegare in questo luogo il numero delle lodi che alla grandezza de i proprii meriti dell'A. V. e della Sua Serenissima Casa si devono, così lungo discorso far mi converrebbe, che il proemio di lunga mano il resto del ragionamento avanzerebbe; onde io mi asterrò di tentare quell'impresa, al mezo della quale, non che al fine, condurmi diffiderei. Oltre che, non per accrescere splendore alla Serenità Vostra, che già come nascente Sole per tutto l'occidente risplende, ho io abbracciata l'occasione di dedicarli la presente fatica, ma, all'incontro, acciò che il fregio e l'ornamento del nome vostro, che in fronte, com'io nell'anima, porterà sempre scritto, all'oscure sue tenebre grazia e splendore aqquisti. Né io come oratore per esaltare la gloria di V. A. S. gli vengo avanti, ma come devotissimo servo ed umilissimo vassallo li porgo un debito tributo; il che prima avrei fatto, se la tenerezza della sua età non mi avesse persuaso ad aspettar questi anni a simili studii più accomodati. Che poi questo picciol dono deva esser con lieta fronte ricevuto dall'A. V., non devo io mettere in dubio; sì perché l'infinita sua umanità nativa me lo persuade, e la proporzione, che ha questa lettura con li altri tanti suoi esercizii regii, me l'afferma; sì ancora, oltre a ciò, perché l'esperienza stessa me l'accerta, essendosi ella, per gran parte dell'estate passata, degnata di ascoltar con tanto benigna udienza dalla mia viva voce l'esplicazione di molti usi di questo Strumento. Gradirà dunque l'A. V. S. questo mio, dirò quasi, scherzo matematico a i suoi primi giovenili studii nobilmente conforme; ed avanzandosi con l'età in queste, veramente regie, discipline, aspetti di tempo in tempo dal mio basso ingegno tutti quei più maturi frutti, che dalla Divina grazia m'è stato e sarà conceduto di raccorre. E qui con ogni umiltà inchinandomi, li bacio reverentemente la vesta; e dal S. Dio li prego somma felicità.

Di Padova, li X di Luglio 1606.

Di V. A. Serenissima

Umiliss. ed Obligatiss. Servo

GALILEO GALILEI.

A I DISCRETI LETTORI

La occasione di pratticar con tanti e tanti Signori grandi in questo nobilissimo Studio di Padova, per instituirgli nelle scienze matematiche, mi ha con lunga esperienza fatto conoscere, come non fu del tutto indecente la richiesta di quel gran discepolo, che da Archimede, suo maestro nella geometria, ricercò strada più facile ed aperta, che all'aqquisto di quella lo conducesse: imperò che anco in questa età pochissimi sono a i quali gli erti e spinosi sentieri, per i quali passar bisogna prima che all'aqquisto de i preziosi frutti di queste scienze pervenir si possa, non rincreschino, o che spaventati dalla lunga asprezza, e più dal non vedere, o potersi imaginare, come queste oscure e sconosciute strade al desiderato termine condur gli possino, a men che mezo il cammino non si atterrino, ed abbandonino l'impresa. E ciò ho io tanto più frequentemente veduto accadere, quanto con più gran personaggi mi sono incontrato; come quelli che, essendo in tanti altri maneggi occupati e distratti, non possono in questi esercitar quell'assidua pazienza, che vi saria necessaria. Io dunque, scusandogli insieme col giovine Re di Siracusa, e desiderando che non restino per la difficoltà e lunghezza delle communi strade privi di cognizioni tanto a nobili Signori necessarie, mi rivolsi a tentare di aprir questa via veramente regia, la quale con l'aiuto di questo mio Compasso in pochissimi giorni insegna tutto quello, che dalla geometria e dall'aritmetica, per l'uso civile e militare, non senza lunghissimi studii per le vie ordinarie si riceve. Quello che io abbia con questa mia opera conseguito, nol dirò io, ma lo lascierò giudicare a quelli che da me sin qui l'hanno appresa o per l'avvenire l'apprenderanno, ed in particolare da chi avrà veduti gli Strumenti da gli altri in simili propositi ritrovati: ben che la più gran parte dell'invenzioni, e le maggiori, che nel mio Strumento si contengono, da altri sin qui non sono state né tentate né immaginate; tra le quali è molto principale questa, del poter qual si voglia persona risolvere in un istante le più difficili operazioni di aritmetica; delle quali però ne descrivo quelle sole che alle civili e militari occorrenze più frequentemente accaggiono. Duolmi solamente, benigno lettore, che quantunque io mi sia ingegnato di spiegare le seguenti cose con ogni chiarezza e facilità possibile, tuttavia a chi le dovrà dalla scrittura cavare, resteranno in qualche oscurità involte, perdendo appresso molta di quella grazia, che nel vederle attualmente operare, e nell'apprenderle dalla viva voce, le rende meravigliose: ma questa è una di quelle materie, che non patiscono di essere con chiarezza e facilità descritte, né intese, se prima dalla viva voce non si ascoltano, e nell'atto stesso esercitar non si veggono. E questa saria stata potente cagione, che mi arrebbe fatto astener dall'imprimer quest'opera, se non mi fosse giunto all'orecchie, che altri, alle mani di cui, non so in qual guisa, è pervenuto uno de i miei Strumenti con la sua dichiarazione, si apparecchiava per appropriarselo; il che mi ha messo in necessità di assicurar, col testimonio delle stampe, non meno le fatiche mie, che la riputazione di chi se l'avesse volute attribuire; perché quanto al far cauto me, non mancano le testimonianze di Principi ed altri gran Signori, i quali da 8 anni in qua hanno questo Strumento veduto, e da me appresone l'uso; de i quali quattro soli mi basterà ora nominare. Uno fu l'Illustrissimo ed Eccellentissimo Sig. Gio. Friderico Principe di Holsazia, etc. e Conte di Oldemburg, etc., che l'anno 1598 apprese da me l'uso di questo Strumento, ma non ancora a perfezione ridotto. E poco doppo fui dell'istesso favore onorato dal Serenissimo Arciduca D. Ferdinando d'Austria. L'Illustrissimo ed Eccellentissimo Sig. Filippo Landgravio di Assia e Conte di Nidda, etc. l'anno 1601 intese il medesimo uso qui in Padova. Ed il Serenissimo di Mantova due anni sono volse da me sentirne l'esplicazione.

Aggiugnesi che il tacere io la fabrica dello Strumento, la quale per la lunga e laboriosa sua descrizione e per altri rispetti al presente pretermetto, renderà questo trattato del tutto inutile a chi senza lo Strumento ei pervenisse nelle mani. E per tal causa ne ho io fatte stampare appresso di me 60 copie sole, per presentarne insieme con lo Strumento, con la somma diligenza che si ricerca fabricato e diviso, prima al Serenissimo Principe di Toscana mio Signore, e poi ad altri Signori, da i quali so questa mia fatica esser desiderata. Finalmente, essendo mia intenzione di esplicare al presente operazioni per lo più attenenti al soldato, ho giudicato esser bene scrivere in favella toscana, acciò che, venendo talora il libro in mano di persone più intendenti della milizia che della lingua latina, possa da loro esser comodamente inteso.

Vivete felici.

DIVISIONE DELLA LINEA

 Operazione I.

Venendo alla dichiarazione particolare delle operazioni di questo nuovo Compasso Geometrico e Militare, primamente faremo principio da quella faccia di esso nella quale sono notate quattro coppie di linee con loro divisioni e numeri; e tra esse parleremo prima delle più interiori, denominate Linee Aritmetiche per esser le loro divisioni fatte in proporzione aritmetica, cioè con eguali eccessi, che procedono sino al numero 250, dalle quali trarremo diversi usi. E primamente:

Col mezo di queste linee potremo dividere una linea retta propostaci in quante parti eguali ne piacerà, operando in alcuno delli infrascritti modi.

Quando la proposta linea sia di mediocre grandezza, sì che non ecceda l'apertura dello Strumento, piglieremo con un compasso ordinario l'intera quantità di quella, e questo spazio applicheremo traversalmente, aprendo lo Strumento, a qualunque numero di esse Linee Aritmetiche, pur che sia tale, che sopra le medesime linee ve ne sia un minore, e da quello contenuto tante volte quante sono le parti in che si ha da dividere la linea proposta; ed aggiustato in tal guisa lo Strumento, e preso lo spazio traversale tra i punti di questo minor numero, questo senz'alcun dubbio dividerà la proposta linea nelle parti ordinateci. Come, per essempio:

Dovendo noi dividere la linea data in cinque parti eguali, pigliamo due numeri de' quali il maggiore sia quintuplo dell'altro, come sariano 100 e 20, ed aperto lo Strumento aggiustiamolo in maniera, che la distanza già presa col compasso si adatti traversalmente alli punti segnati 100.100, e non movendo più lo Strumento, prendasi la distanza pur traversale tra li punti delle medesime linee segnati 20.20; perché indubitatamente questa sarà la quinta parte della linea proposta. E con simile ordine troveremo ogn'altra divisione: avvertendo di prendere numeri grandi, pur che non si passi 250, perché, così facendo, l'operazione riuscirà più facile ed esatta.

L'istesso potremo conseguire operando in un altro modo; e l'ordine sarà tale. Volendo dividere, per essempio, la sottoposta linea AB , v. g., in 11 parti, prenderò un numero multiplice dell'altro undici volte, come saria 110 e 10, e presa col compasso tutta la linea AB, l'accomoderò traversalmente, aprendo lo Strumento, alli punti 110; dipoi, non si potendo sopra le medesime linee prendere la distanza tra li punti 10, li quali vengono occupati dalla grandezza della nocella, in vece di questa si piglierà l'intervallo tra li punti 100.100, stringendo un poco il compasso; del quale fermata poi un'asta nel punto B, noterò con l'altra il segno C, onde la rimanente linea AC sarà la undecima parte di tutta l'AB; e similmente, fermata l'asta del compasso in A, segnerò verso l'altra estremità il punto E, lasciando la EB eguale alla CA. Dipoi, stringendo ancora un poco il compasso, prenderò l'intervallo traversale tra li punti 90.90 e questo trasporterò da B in D, e da l'A in F, ed averò due linee CD, FE, undecime parti ancor'esse della intera. E col medesimo ordine trasferendo di qua e di là le distanze prese tra li punti 80.80, 70.70, etc., troveremo le altre divisioni; come nella sottoposta linea distintamente si vede.

Ma quando ci fusse proposta una piccolissima linea da dividersi in molte parti, come sarebbe, per essempio, la seguente linea AB , per dividerla, v. g., in 13 parti, potremo secondo quest'altra regola procedere.

Prolunghisi occultamente essa linea AB sino in C; e misurate in essa altre linee, quante ci piaceranno, eguali alla AB, e siano nel presente essempio altre sei, sì che AC sia settupla di essa AB, è manifesto che di quelle parti, delle quali la AB contiene tredici, tutta la AC ne conterrà 91; onde, presa con un compasso tutta la AC, l'applicheremo traversalmente, aprendo lo Strumento alli punti 91.91, e, stringendo poi il compasso a un punto meno, cioè a li punti 90.90, trasporteremo questa distanza dal punto C verso A; perché, notando il termine verso A, si lascerà la novantunesima parte di tutta la CA, che è la tredicesima della BA, fuori, pur verso il termine A. E così, se ci piacerà, verremo stringendo di punto in punto il compasso all'89, 88, 87, etc., e trasporteremo questi intervalli dal termine C verso A, e si verranno di grado in grado ritrovando e notando le altre particelle della linea proposta AB.

Ma se finalmente la linea da dividersi fusse lunghissima, sì che eccedesse di molto la maggiore apertura dello Strumento, potremo in ogni modo prendere di essa la parte assegnataci, la quale sia, per essempio, la settima. Ora per trovarla, avendoci prima immaginati due numeri, l'uno settuplo dell'altro, quali sieno, v. g., 140 e 20, costituiscasi lo Strumento in qual si voglia apertura, e da esso presa con un compasso la distanza traversale tra li punti 140.140, veggasi quante volte questa è compresa nella gran linea proposta; e quante volte vi è contenuta, tante volte l'intervallo traversale tra li punti 20.20 si replichi sopra la gran linea, e si averà la sua settima parte, quando però l'intervallo, che si prese tra li punti 140, avesse misurato precisamente la data linea. Ma se non l'avesse misurata a punto, bisogneria prendere dell'avanzo la settima parte, secondo il modo di sopra dichiarato, e questa aggiugnere a quell'intervallo che fu sopra la gran linea più volte replicato; e si averà la settima parte a capello, secondo che si desiderava.

COME DI UNA LINEA PROPOSTA POSSIAMO PRENDERE QUALUNQUE PARTI CI VERRANNO ORDINATE

Operazione II.

La presente operazione è tanto più utile e necessaria, quanto che senza l'aiuto del nostro Strumento saria difficilissimo trovar tali divisioni; le quali però con lo Strumento in uno instante si conseguiranno. Quando dunque ci bisognasse d'una linea proposta prendere qualunque parti ci venissero ordinate, come, per essempio, delle 197 parti doviamo prendere le 113, piglisi senz'altro con un compasso la lunghezza della data linea, ed aperto lo Strumento sin che tale lunghezza si accomodi traversalmente alli punti segnati 197, e più non lo movendo, prendasi con l'istesso compasso la distanza tra li punti 113.113; ché tanta senz'alcun dubio sarà la porzione della linea proposta, che alli centotredici centonovantasettesimi si agguaglia.

COME LE MEDESIME LINEE CI PRESTANO DUE, ANZI INFINITE, SCALE PER TRASPORTAR UNA PIANTA IN UN'ALTRA MAGGIORE O MINORE, SECONDO IL NOSTRO ARBITRIO

Operazione III .

Èmanifesto che qualunque volta ci bisognasse cavare da un dissegno un altro maggiore o minore secondo qual si voglia proporzione, fa di mestiero che ci serviamo di due scale esattamente divise, l'una delle quali ci serva per misurare il disegno già fatto, e l'altra per notare le linee del disegno da farsi, tutte proporzionate alle loro corrispondenti del disegno proposto; e tali due scale avremo sempre dalle linee delle quali ora parliamo: ed una d'esse sarà la linea già sopra lo Strumento dirittamente divisa e ch'ha il suo principio nel centro dello Strumento; e questa, ch'è una scala stabile, ci servirà per misurare i lati della proposta pianta: l'altra, che sarà per disegnare la nuova pianta, deve esser mobile, cioè deve potersi crescere e diminuire ad arbitrio nostro, secondo che la nuova pianta dovrà esser o maggiore o minore; e tale scala mutabile sarà quella che dalle medesime linee avremo traversalmente, stringendo o allargando il nostro Strumento. Ma per più chiara intelligenza del modo d'applicare all'uso tali linee, ne metteremo un essempio.

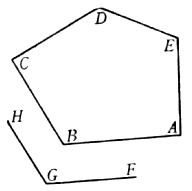Siaci dunque proposta la pianta ABCDE, alla quale se ne deve disegnare un'altra simile, ma sopra la linea FG, la quale sia omologa, cioè risponda alla linea AB. Qui è manifesto che bisogna servirsi di due scale l'una per misurar le linee della pianta ABCDE, e l'altra con la quale si misurino le linee della pianta da farsi, e questa deve esser dell'altra maggiore o minore secondo la proporzione della linea FG alla AB. Piglia dunque con un compasso la linea AB, la quale applica rettamente sopra la scala dello Strumento, ponendo un'asta del compasso nel centro dello Strumento, e l'altra sopra il punto dove cascherà, che sia, per essempio, al 60; dipoi prendi pur col compasso la linea FG, e posta una delle sue aste nel punto 60, apri lo Strumento sin tanto che l'altr'asta caschi giusto traversalmente sopra l'altro corrispondente punto 60: né più si muterà tale costituzione dello Strumento, ma tutti gli altri lati della pianta proposta si misureranno sopra la scala retta, ed immediatamente si prenderanno le distanze corrispondenti ad essi traversalmente, per li lati della nuova pianta. Come, verbi gratia, vogliamo ritrovare la lunghezza della linea GH rispondente alla BC: prendi col compasso la distanza BC, e questa applica dal centro dello Stromento rettamente sopra la scala; e fermata l'altr'asta nel punto dove casca, quale sia, per essempio, 66, volta l'altr'asta all'altro punto 66, traversalmente rispondente, secondo la cui misura taglierai la linea GH, che risponderà alla BC in quell'istessa proporzione che la linea FG alla AB. Ed avvertiscasi, che quando si volesse trasportare una pianta piccola in un'altra assai maggiore, bisognerà servirsi delle due scale con ordine opposto, cioè usare la scala retta per la pianta da farsi, e la traversale per misurar le linee della pianta proposta. Come, per essempio, aviamo la pianta ABCDEF 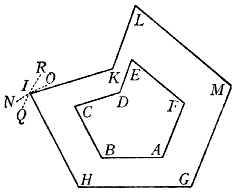, la quale vogliamo trasportare in un'altra assai maggiore, cioè sopra la linea GH che sia rispondente alla linea AB. Per aggiustar le scale prendasi la linea GH, e veggasi quanti punti contiene nella scala retta, e veduto contenerne, v. g., 60, prendasi la sua rispondente AB, ed adattisi traversalmente alli punti 60.60, né più si muova lo Strumento: per trovar poi la linea HI, rispondente alla BC, piglia col compasso essa BC, e va investigando a quali punti si accomodi sopra la scala traversale; e trovato accomodarsi, per essempio, alli punti 46, piglia immediatamente l'intervallo de i punti 46 sopra la scala retta; e troverai la lunghezza della linea HI rispondente alla BC. E notisi, tanto per questa quanto per la precedente operazione, che non basta aver trovato la lunghezza HI, se non si trova ancora a qual punto si deve drizzare, acciò che costituisca l'angolo H eguale all'angolo B. Però, trovata che si averà essa linea HI, fermata un'asta del compasso nel punto H, si noterà con l'altra occultamente una porzione di arco, secondo che mostra la linea puntata OIN; di poi si piglierà l'intervallo tra 'l punto A e 'l punto C, e si cercherà quanti punti sia sopra la scala traversale; e trovato essere, v. g., 89, si prenderà rettamente la distanza 89 col compasso; del quale fermata un'asta in G, si noterà con l'altra l'intersecazione dell'arco RIQ con l'arco primo OIN, fatta nel punto I, al quale si deve drizzar la linea HI: e sarà senza dubio l'angolo H eguale all'angolo B, e la linea HI proporzionale alla BC. E con tale ordine si troveranno li altri punti K, L, M, rispondenti all'angoli D, E, F.

REGOLA DEL TRE RISOLUTA COL MEZO DEL COMPASSO E DELLE MEDESIME LINEE ARITMETICHE.

 Operazione IV.

Servonci le presenti linee non tanto per la resoluzione di diversi problemi lineari, quanto per alcune regole di aritmetica: tra le quali porremo questa, che risponde a quella nella quale Euclide c'insegna. Proposti tre numeri, trovare il quarto proporzionale; perché altro non è la regola aurea, che del tre domandano i prattici, che trovare il quarto numero proporzionale alli tre proposti. Dimostrando adunque il tutto con l'essempio, per più chiara intelligenza, diciamo:

Se 80 ci dà 120, che ci darà 100? Hai dunque tre numeri posti con quest'ordine 80 120 100: e per trovare il quarto numero che cerchiamo, prendi sopra lo Strumento rettamente il secondo numero de i proposti, cioè 120, ed applicalo trasversalmente al primo, cioè all'80; dipoi prendi trasversalmente il terzo numero, cioè 100, e misuralo rettamente sopra la scala; e quello che troverai, cioè 150, sarà il quarto numero cercato. E nota che l'istesso avverria se, in vece di prendere il secondo numero, pigliassi il terzo, e poi, in vece del terzo, pigliassi il secondo; cioè che l'istesso ci darà il secondo numero preso rettamente ed applicato al primo trasversalmente, pigliando dipoi il terzo trasversalmente e misurandolo rettamente, che ci daria il terzo rettamente preso e trasversalmente al primo applicato, pigliando poi il secondo trasversalmente e rettamente misurandolo: ché nell'uno e nell'altro modo troveremo 150. E ciò è bene aver avvertito, perché, secondo le diverse occasioni, questo di quello o quello di questo modo di operare ci tornerà più accomodato.

Possono, circa l'operazione di questa regola del tre, occorrere alcuni casi, li quali potriano partorir qualche difficoltà se non si avvertissero, dimostrando appresso come in essi si deva procedere. E prima, potria alcuna volta occorrere che, delli 3 numeri proposti, né il secondo né il terzo, preso rettamente, si potesse applicare trasversalmente al primo: come se si dicesse: 25 mi dà 60; che darà 75? dove tanto il 60 quanto il 75 passa il doppio del primo, cioè di 25, sì che né l'uno né l'altro di essi si può, rettamente preso, applicare trasversalmente ad esso 25. Onde, per conseguire l'intento nostro, piglieremo o il secondo o il terzo rettamente, e l'applicheremo al doppio del primo trasversalmente, cioè a 50 (e quando non bastasse al doppio, l'applicheremo al triplo, al quadruplo, etc.); dipoi, pigliando l'altro trasversalmente, affermeremo che quello che ci mostrerà misurato rettamente sarà la metà (o vero la terza o quarta parte) di quello che cerchiamo. E così, nel proposto essempio, 60 preso rettamente, applicato al doppio di 25, cioè a 50, trasversalmente, e subito preso il 75, pur trasversalmente, e questo misurato rettamente, troveremo che ci darà 90; il cui doppio, ciò è 180, è il quarto numero che si cercava.

Potria in oltre occorrere che il secondo o il terzo de i numeri proposti non si potesse applicare al primo, per esser esso primo troppo grande, sì che eccedesse il numero segnato sopra le linee, cioè 250: come se dicessimo: 280 mi dà 130; che mi darà 195? In tal caso, preso rettamente il 130, si butterà trasversalmente alla metà di 280, che è 140; dipoi si prenderà trasversalmente la metà del terzo numero, cioè di 195, che è 97 e mezo, e questo spazio, misurato rettamente, ci darà 90 e mezo: che è quello che si cercava.

Un'altra cautela sarà bene che ponghiamo, per servircene quando il secondo o terzo delli numeri proposti fusse molto grande, essendo li altri due mediocri: come quando si dicesse: Se 60 mi dà 390, che mi darà 45? Preso dunque 45 rettamente, si applicherà trasversalmente al 60; e non si potendo pigliare il 390 intero, lo piglieremo in pezzi, secondo che più ci piacerà: come, v. g., piglierò 90 trasversalmente, il quale, misurato rettamente, mi darà 67 e mezo, il che noterò da parte; piglierò poi trasversalmente 100, che, misurato rettamente, mi darà 75; e perché nel 390 vi è una volta 90 e tre volte 100, prenderò tre volte il 75 trovato, e di più 67 e mezo, che fu trovato in virtù del 90; e tutta questa somma fa 292 e mezo, per il quarto numero che si cerca.

Ultimamente non resteremo di dire come si possa operare la medesima regola in numeri picciolissimi, ben che nello Strumento non si siano potuti notare i punti dal 15 in giù, mediante la nocella che unisce e collega le aste dello Strumento. Ma in questa occasione ci serviremo delle decine de i punti come se fussero unità: sì che dicendo, per essempio: Se 10 dà 7, che darà 13? non potendo pigliar 7 per buttarlo a 10, piglieremo 70, cioè 7 decine, e lo butteremo a 10 decine, cioè a 100; e subito pigliando 13 decine, torneremo a misurar questa distanza rettamente, e la troveremo contenere punti 91, che sono 9 ed un decimo, facendo, come si è detto, che ogni decina vaglia uno. E da tutti questi avvertimenti, quando si averanno bene in prattica, si potrà facilmente investigare la soluzione di tutte le difficoltà, che ci potessero in ogni caso occorrere.

REGOLA DEL TRE INVERSA, RISOLUTA COL MEZO DELLE MEDESIME LINEE

Operazione V.

Con non dissimile operazione si risolveranno i quesiti della regola del tre inversa: eccone un essempio. Quella vittovaglia che basteria per mantenere 60 giorni 100 soldati, a quanti basteria giorni 75? Questi numeri, disposti alla regola, stariano in quest'ordine 60 100 75. E l'operazione dello Strumento richiede che pigli rettamente il primo numero, cioè 60, e l'applichi trasversalmente al numero terzo, cioè 75; e non movendo lo Strumento, piglia trasversalmente il 100, che è il secondo, e misuralo rettamente, e troverai 80: qual'è il numero cercato. Dove si deve parimente avvertire, che 'l medesimo ritroveremo applicando il secondo rettamente al terzo trasversalmente, e poi misurando rettamente il primo trasversalmente preso. Devesi oltre a ciò notare, che tutti gli avvertimenti posti sopra circa la regola del tre si devono ancora in questa per l'appunto osservare.

REGOLA PER TRASMUTAR LE MONETE

Operazione VI.

Col mezo di queste medesime Linee Aritmetiche possiamo trasmutar ogni spezie di moneta l'una nell'altra con maniera molto facile e spedita: il che si conseguirà con l'aggiustar prima lo Strumento, pigliando rettamente il prezzo della moneta che vogliamo trasmutare, ed accomodandolo trasversalmente al prezzo di quella in cui si ha da fare la trasmutazione; come, acciò più distintamente il tutto s'intenda, dichiareremo con un essempio. Vogliamo, v. g., trasmutare scudi d'oro in ducati veneziani: e perché il prezzo o valuta dello scudo d'oro è lire 8, e la valuta del ducato lire 6, soldi 4, è necessario (poi che il ducato non è misurato precisamente dalle lire, entrandovi soldi 4) risolvere l'una e l'altra moneta, e valutarla con li soldi, considerando come il prezzo dello scudo è soldi 160, e quello del ducato 124. Per aggiustar dunque lo Strumento alla trasmutazione di scudi d'oro in ducati, piglia rettamente la valuta dello scudo, cioè 160, ed applicala, aprendo lo Strumento, trasversalmente al valore del ducato, cioè a 124, né più moverai lo Strumento: dipoi qualunque somma di scudi proposta trasmuterai in ducati, pigliando la detta somma trasversalmente e misurandola rettamente. Come, per essempio, vogliamo sapere quanti ducati faccino 186 scudi: piglia 186 per traverso e misuralo rettamente, e troverai 240; e tanti ducati faranno li detti scudi.

REGOLA DE GL'INTERESSI SOPRA INTERESSI, CHE ALTRIMENTI SI DICE DE I MERITI A CAPO D'ANNO

 Operazione VII.

Assai speditamente potremo risolvere le questioni di questa regola con l'aiuto delle medesime Linee Aritmetiche, e ciò con due diverse maniere di operare, come con due seguenti essempi faremo chiaro e manifesto. Cercasi quanto siano per guadagnare 140 scudi in 5 anni a ragione di 6 per 100 l'anno, lasciando gl'interessi sopra il capitale e sopra li altri interessi, acciò che continuamente guadagnino. Per trovar dunque quanto cerchiamo, piglia rettamente il primo capitale, cioè 140, e questo butta trasversalmente al 100; e senza mover lo Strumento, piglia subito, pur trasversalmente, la distanza tra li punti 106, che è il 100 con l'interesse, e torna di nuovo ad aprir lo Strumento, e questo intervallo, ch'ultimamente pigliasti col compasso, ributtalo al 100; ed aprendo un poco più il compasso, piglia trasversalmente la distanza tra li punti 106, e di nuovo aperto un poco più lo Strumento, butta questa distanza pur ora trovata al 100; ed aprendo il compasso, piglia il 106; ed in somma va replicando questa medesima operazione tante volte, quanto è il numero de gli anni del merito; ed essendo, nel presente essempio, il merito per anni cinque, devi reiterar l'operazione cinque volte. Ed in ultimo, misurando rettamente l'intervallo ch'averai preso, troverai comprender punti 187 e un terzo: e tanti scudi saranno doventati li 140 posti da principio, col guadagno de i sei per cento, nello spazio di anni cinque. E nota, che se ti tornasse più comodo di servirti, in cambio del 100 e 106, del 200 e 212, come spesse volte occorrerà, il medesimo sarà ritrovato.

L'altro modo di operare non richiede altra mutazione nello Strumento che un solo primo accomodamento; e procedesi così. Servendoci del medesimo quesito posto sopra, per aggiustar lo Strumento piglia 100 col suo primo interesse, cioè 106, rettamente; ed aperto lo Strumento, applicalo trasversalmente al 100, né mai più moverai lo Strumento. Piglia poi trasversalmente la somma de i denari proposta, che fu 140, e misurala rettamente; e vederai già il guadagno del primo anno esser 148 e due quinti, comprendendo però anche il capitale. Per trovar il secondo anno, piglia trasversalmente questo 148 e due quinti, e senz'altro misuralo rettamente; e troverai 157 e un terzo per il secondo anno. Piglia poi questo medesimo numero 157 e un terzo trasversalmente, e torna a misurarlo rettamente; e troverai 166 e tre quarti per il capitale e guadagno del terzo anno. Torna a pigliar questo 166 e tre quarti trasversalmente, e misuralo rettamente; ed averai per il quarto anno 176 e tre quarti. Finalmente piglia questo trasversalmente, e torna a misurarlo rettamente; ed averai per il quinto anno, tra capitale e guadagno, 186 e un terzo. E così, volendo per più anni, andrai replicando l'operazione. E nota, che quando il primo capitale proposto fusse somma tale che eccedesse il numero de i punti 250, segnati sopra le Linee Aritmetiche, devi operare a pezzi, pigliando la metà, il terzo, il quarto, il quinto, o altra parte della somma proposta; ché in fine, pigliando due, tre, quattro, o cinque, o più volte, quello che trovi, verrai in cognizione di quello che desideri.

DELLE LINEE GEOMETRICHE, CHE SEGUONO APPRESSO, E LORO USI; E PRIMA, COME COL MEZO DI ESSE POSSIAMO CRESCERE O DIMINUIRE IN QUALUNQUE DATA PROPORZIONE TUTTE LE FIGURE SUPERFICIALI

Operazione VIII.

Le linee che seguono appresso le Aritmetiche, di sopra dichiarate, sono dette Linee Geometriche, per esser divise secondo la geometrica proporzione procedente sino al 50; dalle quali trarremo diverse utilità: e prima ci serviranno per trovar il lato di una figura superficiale che ad un'altra proposta abbia una data proporzione; come saria, per essempio 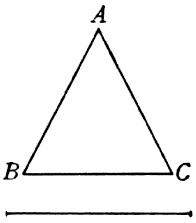, sendoci proposto il triangolo ABC, vogliamo trovar il lato di un altro, che ad esso abbia proporzione sesquialtera. Piglinsi due numeri nella data proporzione, e siano, per essempio, 12 ed 8; e presa con un compasso la linea BC, adattisi, aprendo lo Strumento, alli punti delle Linee Geometriche 8.8, e senza punto muover l'apertura, prendasi l'intervallo tra li punti 12.12; perché, se faremo una linea di tal grandezza lato di un triangolo, rispondente alla linea BC, sarà la sua superficie indubitatamente sesquialtera del triangolo ABC. E questo medesimo intendasi di ogn'altra sorte di figura; e delli cerchi ancora faremo questo medesimo, servendoci delli loro diametri o semidiametri come de i lati delle figure rettilinee. E notisi, per le persone più vulgari, che la presente operazione è quella che c'insegna crescere o diminuire tutte le piante superficiali; come, v. g., avendo una pianta, la quale contiene, per essempio, 10 campi di terreno, ne vorremmo disegnare una che ne contenesse 34. Piglia qualunque linea della pianta di 10 campi, ed applicala trasversalmente alli punti 10 delle presenti Linee Geometriche, e senza più muover lo Strumento, prendi l'intervallo trasversale tra li punti 34 delle medesime linee, e sopra una tal lunghezza descrivi la tua pianta simile alla prima, secondo la regola che di sopra nella terza operazione fu insegnato; ed averai la pianta cercata, capace precisamente di 34 campi.

COME CON L'ISTESSE LINEE POSSIAMO TROVARE LA PROPORZIONE TRA DUE FIGURE SUPERFICIALI TRA DI LORO SIMILI

Operazione IX.

Sianci, per essempio, proposti li due quadrati A, B , o vero qualunque due altre figure, delle quali le due medesime linee A, B siano lati omologhi. Volendo trovar qual proporzione abbino tra di loro le dette superficie, prendasi con un compasso la linea B, la quale, aprendo lo Strumento, si applichi a qual si voglia punto di esse Linee Geometriche, e sia, per essempio, al 20; dipoi, non movendo lo Strumento, prendasi col compasso la linea A, e questa applicata alle Linee Geometriche, veggasi a che numero si adatti; e trovato, v. g., che si aggiusti al numero 10, dirai la proporzione delle due figure esser quella che ha 20 a 10, cioè doppia. E quando la grandezza di questa linea non si accomodasse precisamente ad alcuna delle divisioni, dobbiamo rinovare l'operazione, ed, applicando ad altri punti che alli 20, tentare sin tanto che l'altra linea ancora esattamente si accomodi a qualche punto; il che trovato, sapremo consequentemente la proporzione delle due figure assegnateci, per esser lei sempre la medesima che quella de i numeri delli due punti, alli quali le dette linee, nella medesima apertura dello Strumento, si accomodano. E quando dell'una delle due piante proposteci fusse data la capacità, si troverà il contenuto dell'altra nel medesimo modo. Come, per essempio: Essendo la pianta della linea B 30 campi, si cerca quanto saria la pianta A: accomoda la linea B trasversalmente ai punti 30, e vedi poi a qual numero si adatti, pur trasversalmente, la linea A; e tanti campi dirai contenere la pianta di essa linea A.

COME SI POSSA COSTITUIRE UNA FIGURA SUPERFICIALE SIMILE ED EGUALE A MOLTE ALTRE SIMILI PROPOSTECI 

Operazione X.

Sianci, per essempio, proposte tre figure simili , delle quali li lati omologhi siano le linee A, B, C, alle quali se ne debbe trovar una sola eguale, e pure ad esse simile. Prendi col compasso la lunghezza della linea C, e questa, aperto lo Strumento, applicherai a qual numero più ti piace delle Linee Geometriche, e sia, v. g., applicata alli punti 12.12; dipoi, lasciato lo Strumento in tal sito, prendi la linea B, e vedi a che numero delle medesime linee si accomodi, che sia, per essempio, al 9; e perché l'altra si era aggiustata al 12, congiugnerai questi due numeri 9 e 12 insieme, e terrai a memoria 21; piglia dipoi la terza linea A, e, secondo il medesimo ordine, considera a qual numero delle medesime linee trasversalmente si adatti, e trovato, v. g., adattarsi al 6, aggiugnerai 6 al 21, che salvasti, e averai in tutto 27. Piglia dunque la distanza trasversale tra li punti 27, ed averai la linea D; sopra la quale facendo una figura simile a le altre 3 proposte, sarà ancora di grandezza alle medesime tre insieme eguale. E col medesimo ordine ne potrai ridurre in una sola quante ne venissero proposte, pur che le proposte siano tutte simili tra di loro.

PROPOSTE DUE FIGURE SIMILI E DISEGUALI, TROVAR LA TERZA SIMILE ED EGUALE ALLA DIFFERENZA DELLE DUE PROPOSTE

Operazione XI.

La presente operazione è il converso della già dichiarata nel precedente capitolo; e la sua operazione sarà in tal guisa. Sianci, per essempio, proposti 2 cerchi diseguali 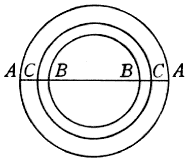, e del maggiore sia diametro la linea AA, e del minore la BB: volendo trovar il semidiametro del cerchio eguale alla differenza delli due A, B, prendi con un compasso la lunghezza della linea maggiore A, ed applicala, aprendo lo Strumento, a qual punto più ti piacerà delle Linee Geometriche, e sia, per essempio, applicata al numero 20; e non movendo lo Strumento, considera a qual punto delle medesime linee si aggiusta la linea B, e trovato, per essempio, accomodarsi al numero 8, sottratto questo di 20, resterà 12; e presa la distanza tra li punti 12.12, averai la linea C, il cui cerchio sarà eguale alla differenza delli due A, B. E quello che si è assemplificato ne i cerchi per via de i loro semidiametri, intendasi esser l'istesso nelle altre figure simili, operando con uno de i loro dati omologhi.

ESTRAZIONE DELLA RADICE QUADRATA CON L'AIUTO DELLE MEDESIME LINEE 

Operazione XII.

Tre differenti modi di operare nell'estrazion della radice quadrata saranno nel presente capitolo dichiarati, uno per li numeri mediocri, uno per li grandi, ed il terzo per li piccioli: intendendo per i numeri mediocri quelli che sono, tanto nel meno quanto nel più, intorno al 5000; maggiori, quelli che sono intorno al 50000; minimi, quelli che sono intorno al 100. E prima faremo principio da i numeri mediocri.

Per estrar dunque e trovar la radice quadrata di un numero mezano proposto, prima devesi aggiustar lo Strumento, la qual cosa sarà con l'accomodare trasversalmente al 16 delle Linee Geometriche lo spazio di 40 punti preso rettamente dalle Linee Aritmetiche: dipoi del numero proposto leva via le due ultime figure, che dinotano le unità e le decine; e quel numero che resta, prendi trasversalmente dalle Linee Geometriche, e misuralo rettamente sopra le Aritmetiche; e quello che trovi sarà la radice quadrata del numero proposto. Come, per essempio, volendo la radice di questo numero 4630, levate le due ultime figure, cioè il 30, resta 46; però piglierai trasversalmente 46 dalle Linee Geometriche e lo misurerai rettamente sopra le Aritmetiche, e lo troverai contenere punti 68, che è la prossima radice cercata.

Ma sono in questa regola da notarsi due cose. La prima è, che quando le due ultime figure, che si levano, passassero 50, devi al numero che resta aggiungere uno: come se, v.g., volessi pigliare la radice di 4192, perché il 92 da levarsi passa 50, in luogo del 41, che restava, devi prendere 42, e nel resto seguire la regola di sopra.

L'altra cautela, che si deve osservare, è che quando quello che resta, detratte le due ultime figure, passasse 50, in tal caso, poi che la divisione delle Linee Geometriche non si estende oltre al 50, si deve del numero che resta prendere la metà o vero altra parte, e questa distanza presa, si deve geometricamente raddoppiare o secondo il numero della detta parte multiplicare; e quell'ultimo intervallo così multiplicato, misurato rettamente sopra le Linee Aritmetiche, ti darà la radice che cerchi. Come, per essempio, vogliamo la radice di 8412: aggiustato, come è detto, lo Strumento, e detratte le due ultime figure, resta 84, il qual numero non è sopra le Linee Geometriche; però piglierai la sua metà, cioè 42: preso dunque lo spazio trasversale tra li punti 42, bisognerà che geometricamente sia raddoppiato, il che farai con aprir più lo Strumento, sin tanto che il detto spazio si adatti a qualche numero del quale sopra le medesime linee ve ne sia uno doppio; come, v. g., saria adattandolo al 20, pigliando poi l'intervallo tra li punti 40, il quale, misurato finalmente sopra le Linee Aritmetiche, ti mostrerà 91 e due terzi in circa, prossima radice del numero 8412 proposto. E se ti fusse bisognato del numero dato pigliare la terza parte, nel triplicarla poi geometricamente, l'applicherai trasversalmente ad un numero delle Linee Geometriche del quale ve ne sia un altro triplo, come saria al 10 per pigliare il 30, o al 12 per pigliar il 36.

Quanto al modo di procedere per i numeri maggiori, non si averà altra differenza dal modo precedente, se non nell'aggiustar lo Strumento e nel levar dal dato numero le tre ultime note. E l'aggiustar lo Strumento si farà pigliando 100 rettamente dalle Linee Aritmetiche, aggiustandolo poi trasversalmente alli punti 10.10 delle Geometriche: il che fatto, volendo, v. g., la radice quadrata di 32140, tolte le tre ultime figure, resta 32, e questo piglierai trasversalmente dalle Linee Geometriche; che, misurato rettamente sopra le Aritmetiche, ti mostrerà 179, prossima radice di 32140. Avvertendo che l'istesse cautele notate nell'operazione precedente si devono per l'appunto osservare in questa: cioè, che quando le tre figure, che si detraggono, passano 500, si ha da aggiunger uno a quello che resta; e se quel che resta passa 50, se ne piglierà una parte, cioè la metà o il terzo, etc., dupplicando o triplicando, al modo dichiarato, quello che averai per la detta parte preso.

Per li numeri minori, aggiusterai lo Strumento secondo il primo modo, cioè con buttare 40 a 16, pigliando poi trasversalmente dalle Linee Geometriche il numero proposto, senza levarne figura alcuna; perché, misurando rettamente il detto spazio sopra le Linee Aritmetiche, troverai la radice cercata in numero intero ed in frazione. Ma nota che le decine delle Linee Aritmetiche ti debbono servire per unità, e le unità per decimi di unità: come, per essempio, vogliamo la radice di 30; aggiusta lo Strumento, come è detto, buttando 40, preso dalle Linee Aritmetiche rettamente, al 16 delle Geometriche trasversalmente, dalle quali, preso transversalmente la distanza delli punti 30, misurandola rettamente sopra le Aritmetiche, troverai punti 55, che importano 5 intieri e 5 decimi, cioè 5 e mezo; quanta è la prossima radice di 30. Avvertendo che in questa regola ancora si devono osservare li avvertimenti e cauzioni nelle altre due regole insegnate.

REGOLA PER LE ORDINANZE DE GLI ESSERCITI DI FRONTE E FIANCO DISEGUALI

 Operazione XIII.

Per le ordinanze di fronte eguale al fianco ci servirà, come è manifesto, l'estrarre la radice quadrata del numero de i soldati propostoci. Ma quando volessimo formare un'ordinanza con una moltitudine assegnata di soldati, della quale la fronte ed il fianco non fussero eguali, ma si rispondessero in una data proporzione, allora, per risolvere il quesito, ci bisogna in altra maniera procedere, operando nel modo che nel seguente essempio si dichiara.

Sendoci dunque ordinato che ritroviamo la fronte ed il fianco di 4335 soldati, messi in ordinanza in maniera che per ogni cinque, che saranno nella fronte, ne siano tre nel fianco, allora, per conseguir l'intento con l'aiuto del nostro Strumento, prima, considerando i numeri della proporzione assegnataci esser 5 e 3, aggiungendo a ciascuno di loro un 0, fingeremo che importino 50 e 30. E per trovar la fronte, prenderemo rettamente con un compasso 50 dalle Linee Aritmetiche, e quest'intervallo accomoderemo trasversalmente alle Linee Geometriche, ed a quel numero che si produce dalla moltiplicazione tra di loro de i numeri della proporzione assegnata, cioè (nel presente essempio) al 15; e lasciato lo Strumento in tale stato, si prenderà trasversalmente, pur nelle medesime Linee Geometriche, la distanza tra li punti segnati dal numero che resta, detratte le decine ed unità dal numero de i soldati propostoci, che nel presente essempio è 43; e misurato tale intervallo rettamente sopra le Linee Aritmetiche, ci darà la fronte di tale ordinanza, che sarà soldati 85. E col medesimo ordine troveremo il fianco, pigliando rettamente 30 dalle Linee Aritmetiche, e buttandolo trasversalmente al 15 delle Geometriche, e da esse immediatamente pigliando, pur trasversalmente, l'intervallo tra li punti 43.43; il quale, misurato rettamente sopra le Linee Aritmetiche, ci darà 51 per il fianco. Ed il medesimo ordine si terrà in ogni altra moltitudine di soldati, ed in qualunque altra proporzione assegnataci: avvertendo che, sì come si disse nella radice quadrata, quando le unità e decine che si levano dal numero proposto passassero 50, si deve alle centinaia, che restano, aggiugnere uno di più, etc. Né voglio tacere come, trovata che si sarà la fronte secondo la regola già dichiarata, si potria con altra regola più spedita, e con le sole Linee Aritmetiche, trovar il fianco, in questa forma operando. Già nell'essempio addotto fu trovato 85 per la fronte, e furno i numeri della proporzione 5 e 3, che è quanto se si dicesse 50 e 30, o vero 100 e 60, etc.: però quello 85, preso rettamente dalle Linee Aritmetiche, accomodisi trasversalmente al 100 delle medesime, e piglisi immediatamente l'intervallo, pur trasversale, tra li punti 60.60 delle medesime linee; il quale, misurato rettamente, ci mostrerà il medesimo numero 51, che nell'altra maniera di operare fu ritrovato.

E questa operazione, che sotto l'essempio delle ordinanze aviamo dichiarata, intendasi esser la regola di uno de i capitoli di algebra, cioè de i censi eguali al numero; onde tutti i quesiti che per esso si risolvono, si scioglieranno anco operando col nostro Strumento nella maniera già dichiarata.

INVENZIONE DELLA MEDIA PROPORZIONALE PER VIA DELLE MEDESIME LINEE

 Operazione XIV.

Con l'aiuto di queste linee e loro divisioni potremo tra due linee, o vero due numeri dati, trovare con gran facilità la linea o il numero medio proporzionale in questa maniera. Siano li due numeri, o vero le due linee misurate proposteci, l'uno 36 e l'altro 16: e presa col compasso la lunghezza dell'una, v. g., della 36, applicala, aprendo lo Strumento, alli punti 36 delle Linee Geometriche, e non movendo lo Strumento, prendi l'intervallo tra li punti 16.16 delle medesime linee, il quale, misurato sopra la medesima scala, troverai esser punti 24; quanto appunto è il numero proporzionale tra 36 e 16. E nota che, per misurar le linee proposte, potremo servirci non solo della scala notata sopra lo Strumento, ma di qualunque altra ancora, quando quella dello Strumento fusse troppo piccola per il nostro bisogno.

Notando in oltre, che quando le linee, ed i numeri che le misurano, tra li quali vogliamo trovare il medio proporzionale, fussero assai grandi, sì che passassero il 50, che è il maggiore numero notato sopra le nostre Linee Geometriche, si potrà nondimeno conseguir l'intento, operando con parti de i proposti numeri, o con altri minori di essi, ma che abbino la medesima proporzione che hanno li primi; e la regola sarà in questo modo. Vogliamo, verbi gratia, pigliare il numero medio proporzionale fra 144 ed 81, li quali eccedono ambidue il cinquanta. Piglisi dalle Linee Aritmetiche 144 rettamente per applicarlo trasversalmente alle Linee Geometriche; ma perché in esse non vi è numero così grande, piglierò imaginariamente una parte di esso numero 144, come saria, v. g., il terzo, cioè 48, e l'intervallo già preso applicherò trasversalmente alli punti 48 delle Linee Geometriche. Dipoi, imaginata la terza parte di 81, che fu l'altro numero dato, la quale è 27, piglierò tal numero pur trasversalmente dalle medesime Linee Geometriche, e questo, misurato rettamente sopra le Aritmetiche, mi darà il medio proporzionale ricercato, cioè 108.

DELLE LINEE STEREOMETRICHE; E PRIMA COME COL MEZO DI ESSE SI POSSIN CRESCERE O DIMINUIRE TUTTI LI CORPI SOLIDI SIMILI SECONDO LA DATA PROPORZIONE

 Operazione XV.

Sono le presenti Linee Stereometriche così dette per esser la lor divisione secondo la proporzione de i corpi solidi, sino a 148; e da esse trarremo molti usi: il primo de i quali sarà il già proposto, cioè come, dato un lato di qual si voglia corpo solido, si possa trovare il lato d'un altro, che ad esso abbia una data proporzione. Come, per essempio , sia la linea A diametro, v. g., d'una sfera, o palla, per dirlo più vulgarmente, o vero lato d'un cubo o altro solido, e siaci proposto di dover trovar il diametro, o lato d'un altro, che a quello abbia la proporzione che ha 20 a 36: piglia col compasso la linea A, ed aprendo lo Strumento, applicala al punto 36 delle Linee Stereometriche; il che fatto, prendi immediatamente l'intervallo tra li punti 20.20, che sarà la linea B, diametro o lato del solido, all'altro, il cui lato A, nella proporzione data di 20 a 36.

PROPOSTI DUE SOLIDI SIMILI, TROVARE QUAL PROPORZIONE ABBINO FRA DI LORO

Operazione XVI.

Non è la presente operazione molto differente dalle dichiarate di sopra, e puossi con gran facilità risolvere. Quando dunque ci venissero proposte le due linee A, B 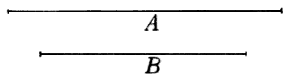, e dimandato qual proporzione abbino fra di loro i lor solidi simili, prenderemo una di esse col compasso; e sia, v. g., presa l'A, la quale applicheremo, aprendo lo Strumento, a qualche numero delle presenti linee, e sia applicata, v. g., al 50.50; e subito presa la lunghezza dell'altra linea B, veggasi a qual numero si accomodi; e trovato adattarsi, per essempio, al 21, diremo il solido A al solido B avere la proporzione di 50 a 21.

PROPOSTI SOLIDI SIMILI QUANTI NE PIACERÀ, TROVARNE UN SOLO EGUALE A TUTTI QUELLI

 Operazione XVII.

Siano proposte le tre linee A, B, C, lati di tre solidi simili 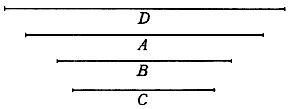; vogliamo trovarne uno eguale a tutti quelli. Per il che fare, prendasi con un compasso la linea A, quale s'applichi a qualche punto delle Linee Stereometriche, e sia, per essempio, al punto 30: e non movendo lo Strumento, considera a qual numero s'adatti la linea B, e trovato, per essempio, adattarsi al 12, aggiugni questo numero al numero 30 già detto, fa 42; il qual numero terrai a memoria: presa dipoi con un compasso la linea C, considera a qual numero delle medesime linee s'accomodi, e sia, per essempio, al 6, e congiunto questo numero con l'altro 42, averemo 48: sì che pigliando l'intervallo tra li punti 48.48, sarà trovata la linea D, il cui solido sarà eguale alli tre proposti A, B, C.

ESTRAZIONE DELLA RADICE CUBA

Operazione XVIII.

Due modi differenti dichiareremo per l'investigazione della radice cuba di qualunque proposto numero.

Il primo ci servirà per i numeri mediocri, e l'altro per i massimi; intendendo per numeri mediocri quelli, da i quali tratte le unità, decine e centinaia, li numeri che restano non eccedono il 148. Per l'estrazione della radice cuba de i quali, prima s'aggiusterà lo Strumento, con l'applicare trasversalmente alli punti 64 delle Linee Stereometriche il 40 preso rettamente dalle Linee Aritmetiche: e fatto questo, leva le 3 ultime note dal numero proposto, e piglia quel che resta dalle Linee Stereometriche trasversalmente, e misuralo rettamente sopra le Aritmetiche, e quello che trovi sarà la radice cuba del numero proposto. Come, v. g., cerchiamo la radice cuba di 80216: aggiustato, come s'è detto, lo Strumento, e tolte via le tre ultime note, resta 80; piglia dunque trasversalmente 80 dalle Linee Stereometriche, e misuralo rettamente sopra le Aritmetiche, e troverai 43; quanta è la radice prossima del dato numero. E nota, che quando, detratte le tre ultime note, restasse più di 148, che è il maggior numero delle Stereometriche, allora potrai operare per parti. Come, per essempio, si cerca la radice cuba di 185840: e perché, detratte le ultime 3 note 840, resta 186 (dico 186, ben che resti 185, perché le centinaia delle tre note detratte sono più di 5, cioè più di mezo migliaio, onde, pigliandolo per un migliaio intero, fo che quel che resta sia 186, cioè uno di più), che eccede il 148, piglieremo la sua metà, cioè 93, trasversalmente dalle Stereometriche già aggiustate; e questo spazio preso si doverà stereometricamente duplicare, cioè applicarlo a qualche numero delle medesime Stereometriche trasversalmente, del qual ne sia uno doppio; e questo, preso pur trasversalmente, e misuratolo sopra la scala Aritmetica, sarà la radice che si cercava. Stando dunque nell'essempio proposto, applicheremo lo spazio, tra li punti 93 già preso, v. g., al 40 delle Linee Stereometriche, pigliando poi l'80, che, misurato sopra le Linee Aritmetiche, ci mostrerà 57; ch'è la prossima radice del numero proposto.

L'altro modo di operare per li numeri massimi sarà con aggiustare lo Strumento applicando la distanza di 100 punti, presa rettamente dalle Linee Aritmetiche, al 100 delle Stereometriche trasversalmente; e sarà aggiustato. Dipoi dal proposto numero devi levare le quattro ultime note, ed il numero che resta prendere trasversalmente da esse Linee Stereometriche, e misurarlo rettamente sopra le Aritmetiche: come, per essempio, sendoci proposto il numero 1404988, avendo già aggiustato lo Strumento al modo detto, e detratte le quattro ultime note, resta 140; il qual numero, preso trasversalmente dalle Linee Stereometriche, e misurato rettamente sopra l'Aritmetiche, ci darà 112, radice prossima del numero proposto. Non ci scordando, che quando le tre note rimanenti importassero più di 148, numero maggiore delle nostre linee, si deve operare per parti, come nell'altra regola superiore fu avvertito.

INVENZIONE DELLE DUE MEDIE PROPORZIONALI

 Operazione XIX.

Quando ci fussero proposti due numeri, o due linee misurate, tra le quali dovessimo trovare due altre medie proporzionali, potremo ciò esseguire facilmente col mezo delle presenti linee; e ciò con questo essempio si farà chiaro.

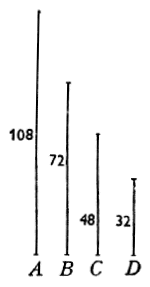
Dove ci vengono proposte le due linee A, D, delle quali l'una sia, per essempio, 108 e l'altra 32: e presa la maggiore con un compasso, adattisi, aperto lo Strumento, alli numeri 108.108; e poi prendasi l'intervallo tra li punti 32.32, il quale sarà la lunghezza della seconda linea B, che, misurata con la medesima scala con la quale furono misurate le proposte linee, si troverà esser 72; e per trovarne la terza linea C, adattisi pure di nuovo, sopra le medesime Linee Stereometriche, la linea B alli punti 108.108, e tornisi di nuovo a pigliare la distanza tra li punti 32.32, che tale sarà la grandezza della terza linea C; e misurata sopra la medesima scala, si troverà essere punti 48. E notisi che non è necessario il prender prima la maggior linea più che la minore; ma nell'uno e nell'altro modo operando, sempre si troverà l'istesso.

COME OGNI SOLIDO PARALLELEPIPEDO SI POSSA COL MEZO DELLE LINEE STEREOMETRICHE RIDURRE IN CUBO

 Operazione XX.

Siaci proposto il solido parallelepipedo, le cui dimensioni siano diseguali, cioè 72, 32 e 84: cercasi il lato del cubo ad esso eguale. Piglia il medio proporzionale fra 72 e 32, nel modo dichiarato di sopra nell'operazione XIV, cioè piglia 72 rettamente dalla scala Aritmetica, e buttalo trasversalmente al 72 delle Linee Geometriche; ma perché non vanno tant'oltre, buttalo alla metà, cioè al 36: e subito prendi pur trasversalmente l'altro numero dalle medesime linee, cioè 32; anzi pur, per dir meglio, piglia la sua metà, cioè il 16 (avendo buttato il primo 72 alla sua metà parimente); e questo che troverai, sarà, come è manifesto, il numero medio proporzionale tra 72 e 32: misuralo dunque sopra le Linee Aritmetiche, e lo troverai esser 48; onde lo butterai trasversalmente a questo medesimo numero 48 delle Linee Stereometriche; e senza muovere poi lo Strumento, prendi pur trasversalmente il terzo numero del solido proposto, cioè l'84, e sarà finita l'operazione, perché facendo questa tal linea lato di un Cubo, quello sarà veramente eguale al solido proposto; e misurandola sopra la scala Aritmetica, la troverai esser 57 e mezo in circa.

ESPLICAZIONE DELLE LINEE METALLICHE NOTATE APPRESSO LE STEREOMETRICHE

 Operazione XXI.

Sono le presenti linee segnate con alcune divisioni, alle quali sono aggiunti questi caratteri: Or. Pi. Ar. Ra. Fe. St. Ma. Pie., che significano Oro, Piombo, Argento, Rame, Ferro, Stagno, Marmo, Pietra. Dalle quali si hanno le proporzioni e differenze di peso, che si trovano fra le materie in esse notate: in guisa che, costituito lo Strumento in qual si voglia apertura, gl'intervalli che cascano fra i punti l'uno all'altro corrispondenti, vengono ad esser diametri di palle, o lati d'altri corpi tra loro simili ed eguali di peso; cioè, che tanto sarà il peso di una palla d'oro il cui diametro sia eguale alla distanza Or. Or., quanto d'una di piombo il cui diametro sia l'intervallo tra li punti Pi. Pi., o una di marmo il cui diametro sia la distanza tra li punti Ma. Ma.

Dal che possiamo in un istante venir in cognizione, quanto grande si doveria far un corpo d'una delle sopranotate materie, acciò fosse in peso eguale ad un altro simile, ma di altra delle materie dette; la qual operazione addimanderemo trasmutazione della materia. Come se, per essempio , la linea A fosse diametro d'una palla di stagno, e noi volessimo trovare il diametro d'un'altra d'oro, a quella in peso eguale, prenderemo con un compasso la linea A, e questa applicata, aprendo lo Strumento, alli punti St. St., piglieremo immediate l'intervallo tra li punti Or. Or.; e tale sarà il diametro della palla di oro, cioè la linea B, eguale all'altra di stagno. Ed il medesimo intendasi di tutti gli altri corpi solidi, e delle altre materie notate. Ma se congiugneremo l'uso di queste linee con quello delle precedenti, ne caveremo molte comodità maggiori; come di sotto si dichiarerà. E prima

CON LE LINEE PREDETTE POTREMO RITROVAR LA PROPORZIONE CHE HANNO IN PESO TRA DI LORO TUTTI LI METALLI ED ALTRE MATERIE NELLE LINEE METALLICHE NOTATE 

Operazione XXII.

Vogliamo, per essempio, trovare qual proporzione abbino fra di loro in peso questi due metalli, argento ed oro. Prendi con un compasso la distanza tra 'l centro dello Strumento ed il punto notato Ar., e questa, aperto lo Strumento, applica a qual più ti piace de i numeri delle Linee Stereometriche, e sia, per essempio, applicata alli punti 100.100; dipoi, senza punto muover lo Strumento, piglia la distanza tra 'l centro del medesimo Strumento ed il punto Or., e questa vedi a che numero s'accomodi sopra le Linee Stereometriche; e trovato, per essempio, adattarsi alli punti 60.60, dirai la proporzione del peso dell'oro a quello dell'argento esser in spezie come 100 a 60. E nota che, nell'operare, li diametri presi ed applicati alle Linee Stereometriche ti mostreranno la proporzione in peso de i loro metalli permutatamente, cioè, come nell'addotto essempio s'è veduto, dal diametro dell'argento ti viene denotato il peso dell'oro, e da quello dell'oro il peso dell'argento: e così venghiamo ad intendere come l'oro è più grave dell'argento a ragione di 40 per 100, essendo che 40 è la differenza tra li due pesi ritrovati per l'oro e per l'argento.

Dal che possiamo venir in cognizione della resoluzione d'un quesito molto bello: che è, propostaci qual si voglia figura di una delle materie notate nelle Linee Metalliche, trovare quanta di un'altra delle dette materie ve ne bisognerà per formarne un'altra a quella eguale; come, v. g., abbiamo una statua di marmo; vorremmo sapere quanto argento v'anderia per farne una della medesima grandezza. Per il che trovare, farai pesare quella di marmo, e sia il suo peso, v. g., 25 libre; poi piglia la distanza tra 'l centro dello Strumento ed il punto Ar., che è la materia della statua futura, e questo applicherai, aprendo lo Strumento, alle Linee Stereometriche, ed al punto segnato col numero del peso della statuetta, cioè alli punti 25.25; e, non movendo lo Strumento, piglierai la distanza tra 'l centro ed il punto Ma., e questa vedrai a che numero, pur trasversalmente, delle Linee Stereometriche si accomodi; e trovato come s'adatta alli punti 96.96, dirai 96 libre d'argento esser necessarie per fare la statua eguale in grandezza all'altra di marmo.

CONGIUGNENDO GLI USI DELLE LINEE METALLICHE E STEREOMETRICHE, DATI DUE LATI DI DUE SOLIDI SIMILI E DI DIVERSE MATERIE, TROVARE QUAL PROPORZIONE ABBINO FRA DI LORO DETTI SOLIDI IN PESO

Operazione XXIII.

Èla linea A diametro d'una palla di rame, e la B diametro di una di ferro; vorremmo sapere qual proporzione hanno fra di loro in peso. 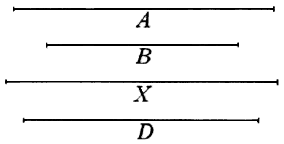Prendi col compasso la linea A, ed aperto lo Strumento applicala alli punti delle Linee Metalliche segnati Ra. Ra.; e senza alterare tal apertura prendi immediatamente la distanza tra li punti Fe. Fe., che sarà quanto la linea X: la quale se sarà eguale alla B, diremo li due solidi A, B essere di peso eguali; ma trovata la X diseguale alla B, ed essendo diametro d'una palla di ferro eguale in peso all'A, è manifesta cosa, che la medesima differenza sarà tra le due palle A, B che è tra l'X, B. E perché X e B sono della medesima materia, troverassi la loro differenza facilmente con le Linee Stereometriche, come di sopra nell'operazione XVI s'è dichiarato: cioè prenderemo la linea X, e l'applicheremo, aprendo lo Strumento, a qualche numero, come, v. g., al 30; il che fatto, si considererà a quale s'aggiusti la linea B; e trovato, per essempio, accomodarsi al 10, diremo la palla di rame A esser tripla della di ferro B.

Il converso della precedente operazione si potrà con pari facilità con le medesime linee ritrovare; cioè, come, dato il peso ed il diametro, o lato, d'una palla, o altro solido, di una delle materie notate sopra lo Strumento, si possa trovare la grandezza d'un altro solido simile, e di qualunque altra delle dette materie, e che pesi qual si voglia peso propostoci. Come, per essempio, essendo la linea X diametro d'una palla di marmo che pesa 7 libre, trovisi il diametro d'una di piombo che ne pesi 20. Qui si vede come doviamo fare due operazioni: l'una, trasmutare il marmo in piombo; e l'altra, crescere il peso di 7 sino al 20. La prima operazione si farà con le Linee Metalliche, accomodando il diametro X alli punti del marmo trasversalmente, pigliando poi, senza muover lo Strumento, l'intervallo tra li punti del piombo, che sarà la grandezza del solido di piombo che peserebbe quanto il proposto di marmo, cioè libre 7. Ma perché volevamo libre 20, ricorreremo all'aiuto delle Linee Stereometriche: ed applicato questo intervallo trasversalmente alli punti 7.7, prenderemo subito la distanza, pur trasversale, tra li punti 20, che sarà eguale alla linea D; la quale senza dubio verrà ad esser il lato della figura solida di piombo, che peserà libre 20.

COME QUESTE LINEE CI SERVONO PER CALIBRO DA BOMBARDIERI ACCOMODATO UNIVERSALMENTE A TUTTE LE PALLE DI QUAL SI VOGLIA MATERIA ED A TUTTI LI PESI

 Operazione XXIV.

Manifestissima cosa è, diverso esser il peso di diverse materie, ed assai più grave esser il ferro della pietra, ed il piombo del ferro; dal che ne séguita, che, dovendosi tirare con l'artigliaria tal ora palle di pietra, altre volte di ferro, o ancora di piombo, il medesimo pezzo che porti tanto di palla di piombo, porterà meno di ferro, e molto meno di pietra, e che, per conseguenza, diverse cariche per le diverse palle se li dovranno dare; laonde quelle sagome, o calibri, sopra i quali fussero notati i diametri delle palle di ferro con li pesi loro, non potranno servirci per le palle di pietra, ma bisognerà che le misure di detti diametri s'accreschino o diminuischino, secondo le diverse materie. In oltre è manifesto che appresso diversi paesi s'usano diversi pesi, anzi che non solamente in ogni provincia, ma quasi in ogni città, sono differenti: dal che ne séguita, che quel calibro, che fusse accomodato al peso d'un luogo, non potrà servirne al peso d'un altro; ma secondo che le libre saranno maggiori o minori in uno ch'in un altro luogo, bisognerà che le divisioni del calibro ottenghino maggiori o minori intervalli. Dal che possiamo concludere, che un calibro che si adatti ad ogni sorte di materia e ad ogni differenza di peso bisogna che per necessità sia mutabile, cioè che si possa crescere e diminuire: e tale a punto è quello che nel nostro Strumento vien segnato, perché, aprendo più o meno, si crescono o diminuiscono gl'intervalli, che tra le divisioni d'esso si ritrovano, senza punto alterar le loro proporzioni.

Ed avendo tali cose in universale dichiarate, passeremo all'applicazione particolare di questo calibro a tutte le differenze di pesi, ed a tutte le materie diverse. E perché non si può venir in cognizione d'alcuna cosa ignota senza il mezo di qualch'altra conosciuta, fa di mestiero che ci sia noto un solo diametro d'una palla di qual si voglia materia, e di qual si voglia peso rispondente alle libre, che nel paese dove vogliamo usare lo Strumento si costumano: dal qual solo diametro verremo, col mezo del nostro calibro, in cognizione del peso di qual si voglia altra palla e di qualunque altra materia; intendendo però delle materie sopra lo Strumento notate.

Ed il modo di conseguir tal cognizione faremo facilmente con un esempio manifesto. Supponghiamo, v. g., esser in Venezia, e di voler quivi servirci del nostro calibro per riconoscer la portata d'alcuni pezzi d'artigliaria; prima procureremo d'aver il diametro ed il peso di una palla di alcuna delle materie sopra detto Strumento segnate; e, per essempio, supporremo d'avere il diametro d'una palla di piombo di libre 10, al peso di Venezia: il qual diametro noteremo con due punti nella costa d'un'asta dello Strumento. Quando dunque vorremo accomodare ed aggiustare il calibro in maniera che, presa la bocca d'un pezzo d'artigliaria, e trasportata sopra esso calibro, conosciamo quante libre di palla di piombo essa porti, non dovremo far altro salvo che prender col compasso quel diametro di 10 libre di piombo, già sopra la costa dello Strumento segnato, ed aprir poi lo Strumento tanto che detto diametro s'aggiusti alli punti delle Linee Stereometriche segnati 10.10: le quali, così aggiustate, ci serviranno per calibro esattissimo; tal che, preso il diametro della bocca di qualsivoglia artigliaria, e trasferitolo sopra detto calibro, dal numero de i punti, a i quali s'adatterà, conosceremo quante libre di palla di piombo porti la detta artigliaria. Ma se volessimo aggiustare lo Strumento sì che il calibro rispondesse alle palle di ferro, allora prenderemo pur l'istesso diametro delle 10 libre di piombo sopra la costa notato, e dipoi l'applicheremo a i punti delle Linee Metalliche segnate Pi. Pi.; e, senza alterare lo Strumento, piglieremo con un compasso l'intervallo tra i punti segnati Fe. Fe., il quale sarà il diametro d'una palla di ferro di 10 libre; e questo diametro, aprendo lo Strumento, s'applicherà a i punti delle Linee Stereometriche, segnati 10.10; ed allora saranno dette linee esquisitamente accomodate per calibro delle palle di ferro. E con simile operazione si aggiusterà per le palle di pietra.

E notisi che, occorrendoci notare sopra la costa dello Strumento diversi diametri di palle rispondenti alle libre di varii paesi, per fuggire la confusione, noteremo sempre diametri di palle di piombo di 10 libre di peso, li quali troveremo esser maggiori o minori secondo la diversità delle libre. Ed il segnare tali diametri, senza obligarci a ritrovare attualmente palle di piombo di 10 libre di peso, non ci sarà difficile, per quello che di sopra nella operazione XXIII si è insegnato: dove, dato un diametro d'una palla di qual si voglia peso e di qualunque materia, s'è veduto come si trovi il diametro d'un'altra d'ogni altro peso e di qual si voglia altra materia, intendendo però sempre delle materie sopra le Linee Metalliche notate; tal che, ritrovandoci noi in qual si voglia paese, pur che troviamo una palla di marmo, di pietra, o d'altra materia sopra lo Strumento segnata, potremo in un subito investigare il diametro di una palla di piombo di 10 libre di peso.

COME, PROPOSTO UN CORPO DI QUAL SI VOGLIA MATERIA, POSSIAMO RITROVARE TUTTE LE MISURE PARTICOLARI DI UNO DI ALTRA MATERIA, E CHE PESI UN DATO PESO

Operazione XXV.

Tra gli usi che da queste medesime linee si possono cavare, uno è questo, col quale possiamo crescere o diminuire le figure solide secondo qual si voglia proporzione, non mutando, o vero mutando, la materia: il che dal seguente essempio s'intenderà. Ci viene presentato un piccolo modello d'artigliaria fatto, v. g., di stagno, e noi aviamo bisogno di cavare da tal modello tutte le misure particolari per un pezzo grande fatto di rame, e che pesi, per essempio, 5000 libre. Prima faremo pesare il piccolo modello di stagno, e sia il suo peso libre 17. Dipoi prenderemo una delle sue misure, qual più ci piacerà, e sia, v. g., la sua grossezza alla gioia, la quale applicheremo, aprendo lo Strumento, alli punti St. St. delle Linee Metalliche (essendo questa la materia del modello propostoci); e perché il pezzo grande deve farsi di rame, prenderemo immediatamente la distanza tra li punti Ra. Ra., la quale saria la grossezza della gioia d'una artigliaria di rame, quando quella dovesse pesare quanto l'altra di stagno. Ma perché deve pesare libre 5000, e non 17 come l'altra, però ricorreremo alle Linee Stereometriche, sopra le quali applicheremo quell'intervallo pur ora preso tra li punti Ra. Ra. alli punti segnati 17.17; e, non movendo lo Strumento, piglieremo l'intervallo de i punti 100.100, che saria la grossezza alla gioia d'un pezzo di 100 libre di peso. Ma noi vogliamo che sia di libre 5000; però questa distanza si deve augumentare secondo la proporzione quinquagecupla: onde, aprendo più lo Strumento, la metteremo a qualche numero, del quale ve ne sia un altro 50 volte maggiore; come saria se l'applicassimo alli punti 2.2, pigliando poi l'intervallo tra li punti 100.100, il quale senz'alcun dubbio sarà la misura della grossezza, che deve darsi alla gioia. E con tal ordine si ritroveranno tutte le misure particolari di tutti li altri membri, come della gola, de gli orecchioni, della culatta, etc.

Né meno resteremo di ritrovare la lunghezza dell'artigliaria, ancorché non possiamo aprire il nostro Strumento sino a tanto spazio. E per trovarla, del piccolo modello non piglieremo l'intera lunghezza, ma solo una sua parte, come saria l'ottava o la decima, etc.; la quale accresciuta con l'ordine pur ora dichiarato, ci rappresenterà in fine l'ottava o decima parte di tutta la lunghezza dell'artigliaria grande.

Ma qui potria per avventura a qualch'uno nascer difficoltà, se dalle nostre Linee Metalliche, nel modo che si sono trovate le dette misure trasmutando l'uno nell'altro metallo semplice, così si potesse far l'istesso in una allegazione di due metalli, come a punto quando nell'essempio sopraposto volessimo formare il pezzo non di rame schietto, ma di metallo misto di rame e di stagno, come anco comunemente si costuma di fare: onde noi, per intera sodisfazione, mostreremo potersi, con l'aiuto delle medesime Linee Metalliche, ritrovare le medesime misure in qual si voglia allegazione, non altrimente che in un semplice metallo. E ciò si farà con l'aggiugner due piccolissimi punti sopra le Linee Metalliche; dico piccolissimi, acciò che ad arbitrio nostro, di poi che ce ne saremo serviti, possiamo cancellarli: e dato, per essempio, che il pezzo dell'artigliaria che vogliamo fare, non di rame puro, come di sopra si suppose, ma di bronzo, dovesse esser gettato, la cui lega fusse per ogni 3 di rame uno di stagno, allora verremo con diligenza dividendo, tanto dall'una quanto dall'altra parte, quella breve linea che è tra li punti segnati Ra. e Sta. in quattro particelle, delle quali tre se ne lascieranno verso lo stagno ed una sola verso il rame, e quivi si farà il punto apparente: del qual punto (segnato, come si disse, tanto nell'una quanto nell'altra Linea Metallica) ci serviremo per la trasmutazione del metallo, non altrimenti che ci servimmo di sopra de i punti Ra. Ra. E con simil regola si potranno, secondo l'occorrenze, segnare nuovi punti di allegazioni di qual si voglino due metalli, e secondo qual si voglia lega.

Ma non saria fuori di proposito e senza comodo notabile, ed in particolare quando s'abbia da fare la trasmutazione in metallo misto ed allegato di due altri secondo qualunque proporzione, l'avertire, che quando si sia trovata una sola delle misure che si ricercano, con l'operare con somma esquisitezza nel modo dichiarato di sopra, si potranno, in virtù di questa unica misura ritrovata, investigare poi tutte l'altre con l'aiuto delle Linee Aritmetiche, con modo non molto differente da quello che nell'operazione terza fu dichiarato. Come, per essempio , era la linea A il diametro, o, vogliamo dire, la grossezza alla gioia, del modello d'artigliaria propostoci; e si trovò la linea B per grossezza della gioia dell'artigliaria di libre 5000, da farsi di metallo che tenga tre di rame e due di stagno. Dico adesso, che per trovar tutte l'altre dimensioni che restano, ci potremo prevalere delle Linee Aritmetiche, pigliando la linea B ed applicandola per traverso a che punto ci piace di esse Linee Aritmetiche, e quanto maggior numero piglieremo, meglio sarà; laonde l'applicheremo, v. g., all'ultimo punto, cioè al 250: e non movendo lo Strumento, vederemo a qual punto s'accomodi, pur trasversalmente, la linea A, che sia, v. g., al 44; dal che vegniamo in cognizione, come, essendo la misura A del modello punti 44, quella che gli ha da rispondere del pezzo reale deve essere 250 de i medesimi punti. E questa medesima proporzione ha da esser osservata in ciascheduna altra misura: onde per trovare, per essempio, la grossezza del pezzo reale nella gola, prenderai tal grossezza dal piccolo modello, ed applicala trasversalmente alli punti 44 delle Linee Aritmetiche, prendendo poi, pur trasversalmente, la distanza fra li punti che sarà la grossezza della gola dell'artigliaria grande. E col medesimo ordine si troveranno tutte l'altre misure.

In oltre per trovare facilissimamente e con somma esquisitezza la linea B prima, che risponda al punto della lega delli due metalli assegnati, si potrà proceder così : ritrovando prima separatamente le due misure semplici, che respondino l'una allo stagno e l'altra al rame, come le due linee CD, CE, delle quali CD sia la misura rispondente al rame puro, e la CE al puro stagno, sì che la differenza loro sia la linea DE, la quale si dividerà secondo la proporzione assegnata per la lega: come, volendo 3 di rame e 2 di stagno, si taglierà la linea DE nel punto F, in maniera che la FE verso lo stagno sia 3 parti, e la FD verso il rame parti 2; che si farà col dividere tutta la DE in cinque parti, lasciandone 3 verso E e 2 verso D: e la linea CF sarà la nostra principale, qual fu poco di sopra la linea B; secondo la ragion della quale, col semplice mezo delle Linee Aritmetiche, si troveranno tutte l'altre misure, senza più ricorrere ad altre Linee Metalliche o Stereometriche, nel modo che si è insegnato nella terza operazione.

DELLE LINEE POLIGRAFICHE, E COME CON ESSE POSSIAMO DESCRIVERE I POLIGONI REGOLARI, CIOÈ LE FIGURE DI MOLTI LATI ED ANGOLI EGUALI

 Operazione XXVI.

Volgendo lo Strumento dall'altra parte, ci si rappresentano le linee più interiori, nominate Poligrafiche dal loro uso principale, che è di descrivere sopra una linea proposta figure di quanti lati ed angoli eguali ci verrà ordinato. E questo facilmente conseguiremo pigliando con un compasso la lunghezza della linea data, la quale si adatterà alli punti segnati 6.6; dipoi, senza muover lo Strumento, piglieremo l'intervallo tra i punti notati col numero che numera i lati della figura che descrivere vogliamo: come, v. g., per descrivere una figura di 7 lati, prenderemo l'intervallo tra li punti 7.7, il quale sarà il semidiametro del cerchio che comprenderà l'eptagono da descriversi; sì che, posta un'asta del compasso ora sopra l'uno ed ora sopra l'altro termine della linea data, faremo sopra di essa un poco d'intersecazione con l'altra, e quivi fatto centro, descriveremo con l'istessa apertura un cerchio occulto, il quale, passando per i termini della data linea, la riceverà 7 volte a punto nella sua circonferenza; onde l'eptagono ne venga descritto.

DIVISIONE DELLA CIRCONFERENZA DEL CERCHIO IN QUANTE PARTI CI PIACERÀ

Operazione XXVII.

Con queste linee si dividerà la circonferenza in molte parti, operando per il converso della precedente operazione, pigliando il semidiametro del cerchio dato, ed applicandolo al numero delle parti nelle quali si ha da dividere il cerchio, pigliando poi sempre l'intervallo de i punti 6.6, il quale dividerà la circonferenza nelle parti che si volevano.

ESPLICAZIONE DELLE LINEE TETRAGONICHE, E COME COL MEZO D'ESSE SI QUADRI IL CERCHIO ED OGNI ALTRA FIGURA REGOLARE, E PIÙ COME SI TRASMUTINO TUTTE L'UNA NELL'ALTRA

Operazione XXVIII.

Sono queste Linee Tetragoniche così dette dal loro uso principale, che è di quadrare tutte le superficie regolari, ed il cerchio appresso; e ciò si fa con facilissima operazione. Imperò che, volendo costituire un quadrato eguale a un dato cerchio, altro non doviamo fare salvo che prendere con un compasso il suo semidiametro, ed a questo, aprendo lo Strumento, aggiustare li due punti delle Linee Tetragoniche segnati con li due piccoli cerchietti; e non movendo lo Stromento, se si prenderà col compasso l'intervallo tra i punti delle medesime linee segnate 4.4, si averà il lato del quadrato eguale al dato cerchio. E non altrimenti, quando volessimo il lato del pentagono, o dello esagono, eguali al medesimo cerchio, si prenderà la distanza tra i punti 5.5, o quella tra i punti 6.6; che tali sono i lati del pentagono, o dell'esagono, eguali al medesimo cerchio.

In oltre, quando volessimo per il converso, dato un quadrato o altro poligono regolare, trovar un cerchio ad esso eguale, preso un lato dal detto poligono, ed accomodatolo al punto delle Linee Tetragoniche rispondente al numero de i lati della figura proposta, si prenderà, senza movere lo Strumento, la distanza tra le note del cerchio; la quale, fatta semidiametro, descriverà il cerchio eguale al dato poligono. Ed in conclusione, con quest'ordine potrassi ritrovare il lato di qual si voglia figura regolare, eguale a qualunque altra propostaci. Come, v. g., dovendo noi costituire un ottangolo eguale a un dato pentagono, s'aggiusterà lo Strumento sì che il lato del pentagono proposto s'accomodi alli punti 5.5; e non mutando lo Strumento, l'intervallo fra li punti 8.8 sarà il lato dell'ottangolo, che si cercava.

COME PROPOSTE DIVERSE FIGURE REGOLARI, BEN CHE TRA DI LORO DISSIMILI, SE NE POSSA COSTITUIRE UNA SOLA EGUALE A TUTTE QUELLE

Operazione XXIX.

La resoluzione del presente problema depende dalla precedente operazione e dalla X di sopra dichiarata. Per ciò che essendoci, v. g., proposte queste figure, un cerchio, un triangolo, un pentagono, ed un exagono, ed imposto che troviamo un quadrato eguale a tutte le dette figure, prima, per l'operazione precedente, troveremo separatamente 4 quadrati eguali alle 4 dette figure; dipoi, col mezo dell'operazione X, troveremo un solo quadrato eguale a quelli 4, il quale senz'alcun dubio sarà eguale alle 4 figure proposte.

COME SI POSSA COSTITUIRE QUAL SI VOGLIA FIGURA REGOLARE EGUALE AD OGN'ALTRA IRREGOLARE, MA RETTILINEA, FIGURA PROPOSTA

Operazione XXX.

La presente operazione è non meno utile che curiosa, insegnandoci il modo, non pure di riquadrare tutte le superficie irregolari, ma di ridurle o in cerchio o in qual si voglia altra figura regolare. E perché ogni rettilineo si risolve in triangoli, quando noi sapremo costituire un quadrato eguale a qual si voglia triangolo, costituendo noi separatamente quadrati particolari eguali a ciaschedun triangolo ne i quali il rettilineo dato si risolve, e poi, con l'operazione X riducendo tutti questi quadrati in un solo, sarà, come è manifesto, ritrovato il quadrato eguale al proposto rettilineo; il qual quadrato col mezo delle Linee Tetragoniche potremo ad arbitrio nostro convertire in un cerchio, in un pentagono, o in altra figura rettilinea regolare. Si è dunque la resoluzione del presente quesito ridotta a dover noi trovare un quadrato eguale a qual si voglia triangolo proposto; il che con modo facilissimo si averà dal lemma seguente.

LEMMA PER LE COSE DETTE DI SOPRA

 Operazione XXXI.

Siaci dunque proposto di dover costituire un quadrato eguale al dato triangolo ABC 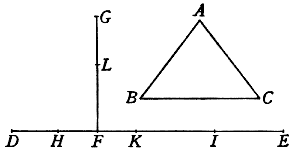. Pongansi da parte due linee ad angoli retti DE, FG: dipoi con un compasso da quattro punte, che da una parte apra il doppio dell'altra, fermata nell'angolo A una delle maggiori aste, slarghisi l'altra sin che, girata intorno, rada la linea opposta BC; dipoi voltando il compasso, notisi con le aste più brevi la distanza FH, che sarà la metà della perpendicolare cadente dall'angolo A sopra il lato opposto BC. Il che fatto, prendasi pure con le maggiori aste la linea BC, la quale si trasporti in FI; e fermata una delle maggiori aste nel punto I, slarghisi l'altra sino al punto H; e volgendo il compasso, senza stringerlo o allargarlo, segnisi con le punte della metà la distanza IK; e fermata una di queste punte in K, taglisi con l'altra la perpendicolare FG nel punto L: ed averemo la linea LF, lato del quadrato eguale al triangolo ABC.

Ma notisi che, se bene aviamo messa questa operazione fatta linealmente senza lo Strumento, non è però che sopra lo Strumento ancora non si possa facilissimamente ritrovare. Imperò che, quando vorremo ridurre qualunque triangolo in quadrato, come, per essempio 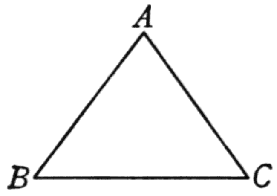, il triangolo ABC, allora, presa dall'angolo A la perpendicolare cadente sopra il lato opposto BC, considereremo sopra la scala Aritmetica quanti punti contenga, e trovato contenerne, v. g., 45, applicheremo questa distanza trasversalmente al 45 dalle Linee Geometriche; pigliando poi la metà della linea BC, considereremo parimente quanti punti della medesima scala Aritmetica essa comprenda, e trovato contenerne, per essempio, 37, piglieremo trasversalmente dalle Linee Geometriche la distanza tra essi punti 37; la quale ci darà la linea LF, il cui quadrato sarà eguale al triangolo ABC.

DELLE LINEE AGGIUNTE PER LA QUADRATURA DELLE PARTI DEL CERCHIO E DELLE FIGURE CONTENUTE DA PARTI DI CIRCUNFERENZE O DA LINEE RETTE E CURVE INSIEME

Operazione XXXII.

Restano finalmente le due Linee Aggiunte, così dette perché aggiungono alle Linee Tetragoniche quello che in esse potria desiderarsi, cioè il modo di riquadrare le porzioni del cerchio e le altre figure che nel titolo si sono dette e più distintamente di sotto si esplicheranno. Sono queste linee segnate con due ordini di numeri, de i quali lo esteriore comincia dal punto segnato con questa nota, seguitando poi li numeri 1, 2, 3, 4, sino in 18; l'altro ordine interiore comincia da questo segno, seguitando poi 1, 2, 3, 4, etc., pur sino a 18: col mezo delle quali linee potremo primamente riquadrare qual si voglia porzione di cerchio propostaci, la quale però non sia maggior di mezo cerchio. E l'uso, acciò meglio s'intenda, con l'essempio s'esplicherà.

Vogliamo, v. g., trovare il quadrato eguale alla porzione del cerchio ABC. Dividasi la sua corda AC nel mezo, nel punto D, e presa con un compasso la distanza AD, s'accomodi, aprendo lo strumento, alli punti segnati; e lasciato lo strumento in tale stato, prendasi l'altezza della porzione, cioè la linea DB, e veggasi a quale de i punti dell'ordine esteriore tale altezza s'accomodi, che sia, per essempio, alli punti segnati 2.2: il che fatto, doviamo con un compasso prender subito l'intervallo tra li punti 2.2 dell'ordine interiore, e sopra una linea di questa grandezza si deve formare il quadrato; che sarà eguale alla porzione ABC. E quando avessimo una superficie contenuta da due porzioni di cerchio simile alla presente figura ABCD, potremo facilmente ridurla in quadrato tirando la corda AC, dalla quale essa figura in due porzioni di cerchio vien divisa; dipoi, per la regola posta di sopra, si troveranno due quadrati eguali alle due porzioni separate, e questi, con l'intervento dell'operazione X, si ridurranno in un solo: e sarà tutto il fatto.

E con non dissimile operazione potrassi riquadrare ancora il settore del cerchio: perché tirata la corda sotto la sua circonferenza sarà tagliato in una porzione di cerchio ed in un triangolo; le quali due parti, per le cose di sopra insegnate, potranno facilmente ridursi in due quadrati, e quelli poi in un solo.

Resta finalmente che mostriamo come le medesime linee ci possin servire per quadrare la porzione maggiore di mezo cerchio, il trapezio contenuto da due rette e due curve, simile a quello della figura appresso ABCD, e la lunula simile alla X 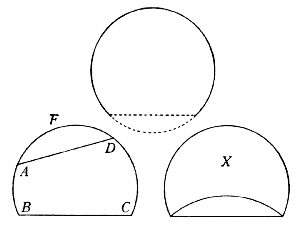; le quali tutte operazioni hanno la medesima resoluzione. Per ciò che, quanto alla porzione maggiore del cerchio, se noi quadreremo la rimanente porzione minore, al modo di sopra insegnato, e tale quadrato caveremo dal quadrato eguale a tutto 'l cerchio, il quadrato eguale al rimanente sarà ancora, com'è manifesto, egual alla maggior porzione del cerchio. Parimente, di tutta la porzione BAFDC trovatone il quadrato eguale, e da esso trattone il quadrato eguale alla porzione AFD, il quadrato rimanente pareggerà il trapezio. E similmente procedendo nella lunula X, tirata la comune corda delle due porzioni di cerchio, si prenderanno separatamente i quadrati ad esse porzioni eguali; la differenza de i quali sarà il quadrato eguale alla lunula. Come poi delli due quadrati proposti si possa trovare la differenza ridotta in un altro quadrato, si è di sopra, nell'operazione XI, con l'intervento delle Linee Geometriche, dichiarato.

DELLE OPERAZIONI DEL QUADRANTE

 Aggiugnendo allo Strumento il Quadrante, nella sua minore circonferenza abbiamo la Squadra da bombardieri, divise, secondo il solito, in punti 12. L'uso ordinario della quale è che si metta una sua costa nel vacuo del pezzo, avendo prima sospeso il filo col perpendicolo dal centro dello Strumento; il qual filo ci mostrerà, segando detta circonferenza, quanta elevazione abbia il pezzo, cioè se 1 punto, o 2, o 3.

E perché l'usar la Squadra in questa maniera non è senza pericolo, dovendo, con l'uscir fuori de i gabbioni o ripari, scoprirci alla vista dell'inimico, per ciò s'è pensato un altro modo di far l'istesso con sicurtà, cioè con l'applicare la Squadra presso al focone del pezzo. Ma perché l'anima di dentro non è parallela con la superficie di fuori, essendo il metallo più grosso verso la culatta, bisogna supplire a tal difetto con l'allungare quell'asta della Squadra che riguarda verso la gioia, aggiugnendovi la sua zanca mobile: il che si farà aggiustando prima una sol volta il pezzo a livello, e poi, posando verso il focone la Squadra, con la zanca allungheremo il piede anteriore, sin che il perpendicolo seghi il punto 6, e fermata la zanca con la sua vite, segneremo una lineetta sopra la costa dello Strumento, dove viene a terminar la cassella della detta zanca, acciò in ogni occasione la possiamo mettere a segno. E poi se vorremo dar un punto d'elevazione, bisognerà alzar il pezzo tanto che il filo seghi il numero 7; se vorremo 2 punti, doverà segar l'8, etc.

La divisione che segue appresso è il Quadrante astronomico: l'uso del quale, essendo stato trattato da altri, non sarà qui dichiarato altrimente.

L'altra circonferenza che segue appresso, e che si vede divisa da alcune linee trasversali, è per prender l'inclinazione della scarpa di tutte le muraglie, cominciando da quelle che avranno per ogni 10 d'altezza uno di pendenza, sino quelle che abbino uno di pendenza per ogn'un e mezo d'altezza.

Volendo servirci di tale Strumento, doviamo sospender il filo da quel piccolo foro che si vede al principio della Squadra da bombardieri; dipoi, accostandoci alla muraglia pendente, gli applicheremo sopra la costa opposta dello Strumento, avvertendo dove taglierà il filo: perché, segando, per essempio, il numero 5, diremo quella tal muraglia aver per ogni 5 braccia d'altezza 1 di pendenza; similmente, tagliando il numero 4, diremo aver 1 di pendenza per ogni 4 d'altezza.

DIVERSI MODI PER MISURAR CON LA VISTA; E PRIMA, DELLE ALTEZZE PERPENDICOLARI, ALLA RADICE DELLE QUALI SI POSSA ACCOSTARE E DISCOSTARE

L'ultima circonferenza, divisa in 200 parti, è una scala per misurar altezze, distanze e profondità col mezo della vista. E prima, cominciando dall'altezze, mostreremo diverse maniere di misurarle, facendo principio dall'altezze perpendicolari, alla radice delle quali ci possiamo accostare. Come saria se volessimo misurar l'altezza della torre AB : venendo nel punto B, ci discosteremo verso C, caminando 100 passi o 100 altre misure, e fermatici nel luogo C, traguarderemo con una costa dello Strumento l'altezza A, come si vede secondo la costa CDA, notando i punti tagliati dal filo DI; i quali se saranno nel centinaio opposto all'occhio, come si vede nell'essempio proposto per l'arco I, quanti saranno detti punti, tanti passi (o altre delle misure che aremo misurate in terra) diremo contenere l'altezza AB. Ma se il filo taglierà l'altro centinaio, come si vede nella seguente figura 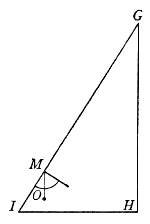, volendo misurar l'altezza GH, sendo l'occhio in I, dove il filo taglia i punti MO, allora, preso il numero di detti punti, divideremo per esso il numero 10000, e l'avvenimento sarà il numero delle misure che nell'altezza GH si conterranno: come, v. g., se il filo avesse tagliato il punto 50, dividendo 10000 per 50, aremo 200; e tante saranno le misure dell'altezza GH.

E perché aviamo veduto che alle volte il filo segherà il centinaio opposto alla costa per la quale si traguarda, e tal volta ancora taglierà il centinaio contiguo a detta costa, e questo potrà avvenire in molte delle operazioni seguenti, però per regola universale s'avvertirà sempre, che quando il filo taglierà il primo centinaio contiguo a detta costa, si deve dividere 10000 per il numero tagliato dal filo, seguendo poi nel resto dell'operazione la regola che sarà scritta: per che noi ne gli essempi seguenti supporremo sempre che il filo tagli l'altro centinaio.

Ma acciò che tanto più si scorga la moltitudine de gli usi di questo nostro Strumento, voglio che i computi più laboriosi, che nelle regole per misurar con la vista ci occorreranno, siano senza fatica alcuna e con somma brevità ritrovati col mezo del compasso sopra le Linee Aritmetiche. E facendo principio dalla presente operazione, per quelli che non sapessero partire 10000 per quel numero tagliato dal perpendicolo, dico che si pigli rettamente sempre 100 dalle Linee Aritmetiche, e che trasversalmente s'accomodi al numero de i punti tagliati da esso perpendicolo, pigliando poi, pur trasversalmente, senza muover lo Strumento, la distanza tra i punti 100; la quale, misurata rettamente, ci darà l'altezza cercata. Come, v. g., se il filo avesse tagliato a 77, pigliando dalle Linee Aritmetiche 100 rettamente, applicalo trasversalmente al 77, e subito prendi, pur trasversalmente, l'intervallo tra i punti 100, e torna a misurarlo rettamente, e troverai contenere punti 130; e tante misure dirai contenersi nell'altezza che misurar volevamo.

In altra maniera potremo misurar una simil altezza, senza obligarci a misurar in terra le 100 misure, nel modo che si farà manifesto. Come se, per essempio 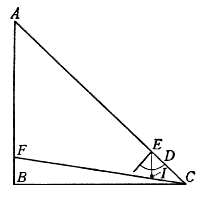, volessimo dal punto C misurar l'altezza della torre AB, drizzando la costa dello Strumento CDE alla sommità A, noteremo li punti tagliati dal filo EI, quali siano, per essempio, 80; dipoi, senza muoverci di luogo, abbassando solamente lo Strumento, traguarderemo qualche segno più basso che sia posto nella medesima torre, come saria il punto F, notando il numero de i punti tagliati dal filo, il quale sia, v. g., 5; veggasi poi quante volte questo minor numero 5 sia contenuto nell'altro 80 (che è 16 volte): e 16 volte diremo la distanza FB esser contenuta in tutta l'altezza BA. E perché il punto F è basso, potremo tale altezza FB con un'asta o altro facilmente misurare, e così venir in cognizione dell'altezza BA. Avvertendo che, nel misurar l'altezze, noi ritroviamo e misuriamo solamente l'altezze sopra l'orizonte del nostr'occhio; tal che quando detto occhio sarà più alto della radice o base della cosa misurata, bisognerà aggiugner all'altezza trovata per via dello Strumento, quel tanto di più che l'occhio sopravanza detta radice.

Il terzo modo di misurar una simile altezza sarà con l'alzarci ed abbassarci. Come 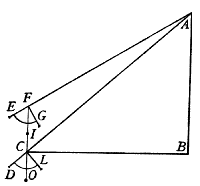, volendo misurar l'altezza AB, costituendo lo Strumento in qualche luogo elevato da terra, come saria nel punto F, traguarderemo secondo la costa EF il punto A, notando i punti G, I tagliati dal filo, quali siano, per essempio, 65; dipoi, scendendo al basso, e venendo perpendicolarmente sotto 'l punto F, come saria nel punto C, traguarderemo la medesim'altezza secondo la costa DC, notando i punti L, O, quali saranno più de gli altri, come, v. g., 70; dipoi prendasi la differenza tra questi due numeri 65 e 70, che è 5; e quante volte essa è contenuta nel maggior de i detti numeri, cioè in 70 (che vi sarà contenuta 14 volte), tante volte diremo l'altezza BA contenere la distanza CF: la quale misureremo, potendolo noi fare comodamente, e così verremo in cognizione di tutta l'altezza AB.

E volendo noi misurar un'altezza la cui radice non si vedesse, come saria l'altezza del monte AB 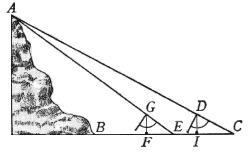, sendo nel punto C, traguarderemo la sommità A, notando i punti I tagliati dal perpendicolo DI, i quali siano, per essempio, 20; di poi, accostandoci verso il monte 100 passi innanzi, venendo nel punto E, traguarderemo l'istessa sommità, notando i punti F, i quali siano 22: il che fatto devonsi multiplicare tra loro questi due numeri 20 e 22; fanno 440: e questo si divida per la differenza delli medesimi numeri, cioè per 2; ne viene 220: e tanti passi diremo esser alto il monte.

Il computo si troverà sopra lo Strumento, pigliando il minor numero de i punti tagliati rettamente sopra le Linee Aritmetiche, ed applicandolo poi trasversalmente alla differenza delli due numeri de i punti, pigliando in oltre trasversalmente l'altro numero de i punti, il quale, misurato rettamente, ci darà l'altezza cercata. Come se, per essempio, i punti tagliati fussero stati 42 e 58, preso 42 rettamente, buttisi trasversalmente alla differenza de i detti numeri, cioè al 16, o, non potendo, al suo doppio, triplo, quadruplo, etc.; sia al quadruplo, che è 64: e preso poi il 58, o il suo quadruplo, cioè 232, e misurato rettamente, ci darà 152 e un quarto, che è il proposito.

Possiamo in oltre col medesimo Strumento misurare un'altezza posta sopra un'altra; come se volessimo misurare l'altezza della torre AB, posta sopra 'l monte BC. 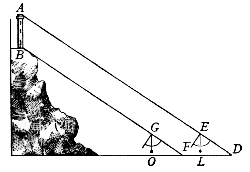Prima, sendo nel punto D, traguarderemo la sommità della torre A, notando i punti tagliati dal filo EI, li quali siano, v. grat., 18; poi, lasciando un'asta piantata nel punto D, venghiamo avanti sin tanto che, traguardando la base della torre, cioè il punto B, il perpendicolo GO tagli il medesimo numero 18, il che sia quando saremo venuti al punto F; dipoi misurinsi i passi tra le due stazioni D, F, quali siano, per essempio, 130: e questo numero si multiplichi per i 18 punti; ne verrà 2340: il qual numero si divida per 100; ne viene 23 e due quinti: e tanti passi sarà alta la torre AB.

Il computo sopra lo Strumento si farà col pigliar rettamente il numero de i passi, o quello de i punti, applicandolo poi trasversalmente al 100, prendendo poi l'altro pur trasversalmente, e misurandolo rettamente. Come se, v. g., i punti fossero stati 64 ed i passi 146, preso 64 rettamente, ed applicatolo trasversalmente al 100, e preso poi trasversalmente 146, e misuratolo rettamente, ci darà 93 e mezo in circa; quanta è l'altezza che si cercava.

Quanto alle profondità, due modi averemo per misurarle. Ed il primo sarà per misurar la profondità contenuta tra le linee parallele, come saria la profondità d'un pozzo, o vero l'altezza d'una torre, quando noi fussimo sopra di essa. Come, per essempio

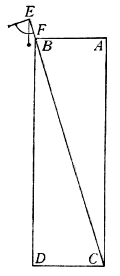
, sia un pozzo ABDC, contenuto tra le linee parallele AC, DB: e voltando l'angolo dello Strumento verso l'occhio E, si traguardi secondo la costa EF, in maniera che il raggio della vista passi per li punti B, C, notando il numero tagliato dal filo, il quale sia, verbi gratia, 5; e poi si consideri quante volte questo numero 5 entra in 100: e tante volte diremo la larghezza BA esser contenuta nella profondità BD.

L'altro modo sarà per misurar una profondità della quale non si vedesse la radice; come se fussimo sopra 'l monte BA, e volessimo misurar la su' altezza sopra 'l piano della campagna. In tal caso alziamoci sopra 'l monte, salendo sopra qualche casa, torre o albero, come si vede nella presente figura 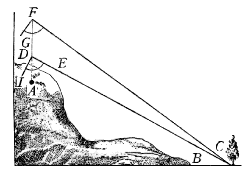, e constituendo l'occhio nel punto F, traguarderemo qualche segno posto nella campagna, come si vede per il punto C, notando i punti tagliati dal filo FG, che siano, v. g., 32; dipoi, scendendo nel punto D, traguardisi il medesimo segno C con la costa DE, notando parimenti i punti A, I che siano 30; e presa la differenza di questi due numeri, cioè 2, veggasi quante volte entra nel minor delli due numeri; e veduto che vi entra 15 volte, diremo l'altezza del monte essere 15 volte più dell'altezza FD: la quale, potendola noi misurare, ci farà venire in notizia di quanto cercavamo.

Passando al misurar le distanze, come saria una larghezza di un fiume, venendo sopra la ripa o altro luogo eminente, sì come nell'essempio si vede 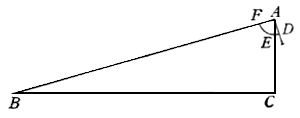; nel qual, volendo noi misurar la larghezza CB, venendo nel punto A, traguarderemo con la costa AF l'estremità B, notando i punti D, E tagliati dal perpendicolo, quali siano, verbi gratia, 5; e quante volte questo numero entra in 100, tante volte diremo l'altezza AC entrare nella larghezza CB: misurando dunque quanta sia tale altezza AC, e pigliandola 20 volte, averemo la larghezza cercata.

Possiamo in altro modo misurare una simile distanza. Come, per essempio 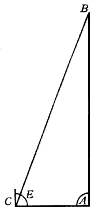, sendo noi nel punto A, vogliamo trovare la distanza sino al punto B: costituiscasi lo Strumento in piano, ed una delle sue coste sia drizzata verso il punto B, e secondo la dirittura dell'altra costa traguardisi verso il punto C, misurando verso la dirittura AC 100 passi o altre misure, e lascisi piantata nel punto A un'asta, ed un'altra si ponga nel punto C; dipoi, venendo nel punto C, si dirizzi una costa dello Strumento verso A, e per l'angolo C si traguardi il medesimo segno B, notando sopra il Quadrante qual punto venga segato dal raggio della vista, che sia il punto E; e preso tal numero, dividasi per esso 10000: e quello che ne verrà, sarà il numero de i passi o altre misure, che saranno tra il punto A ed il segno B.

Ma quando non ci fusse permesso di poter moverci le 100 misure sopra una linea che facesse angolo retto col primo traguardo, in tal caso procederemo altrimenti. Come, v. g. 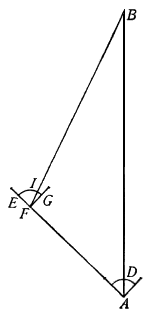, essendo noi nel punto A, e volendo pigliare la distanza AB, né potendo caminare per altra strada che per la AE, la quale con la dirittura AB fa angolo acuto, per conseguire ad ogni modo il nostro intento, aggiusteremo una costa dello Strumento prima alla strada, come si vede per la linea AF, e senza mover lo Strumento, traguarderemo per l'angolo A il punto B, notando i punti tagliati dal raggio AD, quali siano, per essempio, 60; dipoi, lasciando nel punto A un'asta, ne faremo mettere sopra la linea AE un'altra lontana 100 passi, quale sia nel punto F, dove costituiremo l'angolo dello Strumento, aggiustando la costa EF all'asta A, e per l'angolo F traguarderemo il medesimo segno B, notando i punti G, I, quali siano, v. gra., 48. Volendo dunque da questi numeri 60 e 48 trovare la lontananza AB, multiplica il primo in se stesso; fa 3600; aggiugnili poi 10000; fa 13600: e di questo numero piglia la radice quadrata; sarà 117 in circa: e questa multiplica per 100; fa 11700; e finalmente dividi questo numero per la differenza delli due primi numeri 60 e 48, cioè per 12; ne verrà 975: e tanti passi senz'alcun dubio sarà la distanza AB.

Troverassi la calculazione di questa operazione sopra lo Strumento come nel sottoposto essempio s'espone. Siano, v. g., i punti tagliati da i due raggi, l'uno 74 e l'altro 36: e per trovare detto computo, aggiusta prima lo Strumento sì che le Linee Aritmetiche siano tra di loro ad angoli retti; il che farai col prendere 100 punti rettamente da esse, e questi applicare col compasso alle medesime trasversalmente, in maniera che, posta una delle aste nel punto 80, l'altra caschi nel 60 (e questa regola d'aggiustare le dette linee a squadra si tenga a memoria per altri bisogni): fatto questo, prendi la distanza trasversale tra 'l punto 100 ed il maggiore de i due numeri tagliati da i raggi, che qui è 74; la qual distanza presa devi aggiustare trasversalmente alla differenza de i due numeri de i punti tagliati da i raggi, che qui è 38; e se non potessi per la piccolezza di questo numero, serviti del suo doppio, triplo o quadruplo; e qui, per essempio, applicala al suo triplo, che è 114: ed immediatamente piglia la distanza pur trasversale tra li punti 100; la quale misurata rettamente, e presa una, due, tre o quattro volte, ti darà la distanza cercata. Misurala dunque nel presente essempio, e troveraila 109: sì che triplicata ti darà 327, quanta prossimamente è la distanza che misurar volevamo.

Séguita che veggiamo il modo di misurar l'intervallo tra due luoghi da noi lontani: e prima diremo del modo quando da qualche sito potessimo vederli ambidue per la medesima linea retta. Come mostra il presente essempio : nel quale volendo noi misurar l'intervallo tra i punti B, A, stando nel punto C, di dove appariscono per la medesima linea CBA, prima, aggiustata un'asta dello Strumento a tale dirittura, si traguarderà per l'altro verso D, dove pianteremo un'asta lontana dal punto C 100 misure, avendone una simile piantata nel punto C; e venendo al luogo D, aggiusteremo una costa dello Strumento alla dirittura DC, traguardando per l'angolo D li due luoghi B, A, e notando i numeri tagliati da' raggi, che siano, per essempio, 25 e 20; per i quali due numeri si deve dividere 10000: e la differenza delli due avvenimenti sarà la distanza BA.

Ma se volendo noi misurar la distanza tra i due luoghi C, D, non potessimo venir in sito tale che l'uno e l'altro ci apparisse per la medesima dirittura, in questo caso procederemo come appresso si dirà. Sia dunque che, stando noi nel luogo A 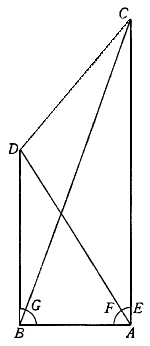, vogliamo investigare la lontananza tra i due luoghi C, D. Prima, aggiustata una costa dello Strumento al punto C, come si vede per la linea AEC, traguardisi per l'angolo l'altro punto D, notando i punti E, F tagliati dal raggio AFD, che siano, v. g., 20; e senza muover lo Strumento, si traguardi per l'altra costa verso 'l punto B, lasciando in A un'asta, ed un'altra facendone porre sopra la dirittura AB: di poi, caminando per tale dirittura, verremo in B, discostandoci dall'altr'asta tanto che, ricostituita una costa dello Strumento sopra la linea BA, l'altra costa ferisca il punto D, come apparisce per la linea BD; e dall'angolo B traguarderemo il punto C, notando il numero tagliato dal raggio BG, che sia, v. g., 15: finalmente si misureranno i passi tra le due stazioni A, B, quali siano, per essempio, 160. E venendo all'operazione aritmetica, prima si multiplicherà il numero de i passi tra le due stazioni, cioè 160 per 100; fa 16000: e questo si deve divider per i 2 numeri de i punti separatamente, cioè per 20 e per 15; e ne verranno i due numeri 800 e 1067: de i quali se ne deve pigliar la differenza, che è 267: e questa si deve multiplicar in se stessa; fa 71289: e questo numero si deve aggiugnere al quadrato del numero de i passi, cioè di 160, che è 25600; ed in tutto farà 96889: del qual numero si deve prendere la radice quadrata, che è 311: e tanti passi diremo essere tra li due luoghi C, D.

Come poi si possa ritrovare il computo sopra lo Strumento, faremo col sottoposto essempio manifesto. Siano, v. g., li due numeri tagliati da i raggi 60 e 34, ed il numero de' passi 116. E venendo all'operazione, prendi sempre 100 dalle Linee Aritmetiche rettamente, ed applicalo trasversalmente al maggior numero de i due tagliati da i raggi, che qui è 60; e subito prendi pur trasversalmente il numero de i passi, che qui è 116, e questo intervallo accomoderai trasversalmente all'altro numero de i raggi, che qui è 34; e se non puoi, applicalo al suo doppio, triplo, quadruplo, o quello che più ti tornerà comodo: sia per ora al suo quadruplo, cioè al 136. Il che fatto, prendi trasversalmente il numero che è la differenza tra li due numeri de i raggi, che qui è 26; o pure piglia il suo doppio, triplo o quadruplo, secondo che poco fa si fece l'applicazione; onde in questo caso devi pigliare il suo quadruplo, cioè 104: e questa distanza misurerai rettamente, salvando in memoria il numero che essa conterrà, che nel presente essempio sarà 148. Aggiusta finalmente le Linee Aritmetiche a squadra al modo di sopra dichiarato: il che fatto, piglia trasversalmente l'intervallo tra 'l numero che salvasti in memoria ed il numero de i passi, cioè tra 'l 148 da una parte ed il 116 dall'altra; e questo misura rettamente, e troverai 188: quanta a punto è la distanza cercata DC.

E finalmente, quando noi non potessimo moverci nella maniera che ricerca la passata operazione, potremo pure nondimeno trovare la lontananza tra due luoghi da noi distanti in altra maniera: ed il modo sarà tale. Sendo noi, per essempio, nel punto C 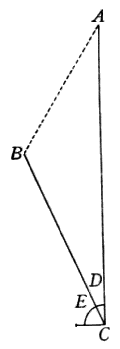, e volendo ritrovar la distanza tra i due luoghi A, B, prima, secondo alcuno de i modi dichiarati di sopra, misuriamo separatamente le distanze tra 'l punto C e l'A, e l'altra tra l'istesso C ed il punto B, e sia, per essempio, la prima passi 850, e l'altra 530; e venendo nel segno C, aggiustando una costa dello Strumento al punto A, come si vede per la linea CDA, traguardisi per l'angolo C l'altro termine B, notando il numero de i punti D, E tagliati dal raggio, che siano, v. g., 15. Multiplica poi questo numero in se stesso; fa 225: ed a questo aggiugni 10000; fa 10225: del quale prendi la radice quadrata, che è 101: multiplica poi la minor distanza, cioè 530, per 100; fa 53000: il quale si divida per la radice pur ora trovata; ne viene 525: e questo multiplica per la maggior distanza, cioè per 850; fa 446250: il qual numero deve esser finalmente duplicato; fa 892500: dipoi devonsi multiplicar separatamente le due distanze ciascuna in se stessa; fanno 722500, e 280900: e questi numeri si devono congiugnere insieme; fanno 1003400: del qual numero si caverà quel duplicato di sopra, cioè 892500; resterà 110900: la cui radice, che è 347, sarà la distanza desiderata tra gli due luoghi A, B.

Con notabil diminuzione di fatica potremo fare il computo presente sopra le Linee Aritmetiche; ed il modo si farà con un essempio manifesto. Pongasi che la maggior distanza sia stata passi 230, e la minore 104, ed il numero de i punti tagliati dal raggio 58. Metti le Linee Aritmetiche a squadra, e posta un'asta del compasso nel punto 100, slarga l'altra in traverso sino al numero de i punti tagliati dal raggio, che qui è 58, e considera quanto è questo spazio misurato rettamente, e lo troverai esser prossimamente 116, il che salva in mente: piglia poi rettamente il detto numero 58, che fu de i punti tagliati dal raggio, ed apri lo Strumento sin che questa distanza s'aggiusti in traverso tra il punto del 100 e quello del 116, che salvasti in mente; e non movendo più lo Strumento, prendi col compasso la distanza trasversale tra li due numeri de i passi, cioè 230 e 104; e questa misurata rettamente, ti darà infine punti 150, quanta è veramente la distanza AB.

Queste sole regole per misurar con la vista ho giudicato, discreto lettore, bastar per ora aver descritte; non che secondo queste sole si possa col presente Strumento operare, essendocene moltissime altre, ma per non mi diffondere in lunghi discorsi senza necessità, essendo sicuro che qualunque di mediocre ingegno averà comprese le già dichiarate, potrà per se stesso ritrovarne altre, accomodate ad ogni caso particolare che occorrer gli potesse.

Ma non solamente avrei potuto diffondermi più assai nelle regole del misurar con la vista, ma molto e molto più ampliarmi nel mostrare la resoluzione, posso dire, d'infiniti altri problemi di geometria e di aritmetica, i quali con le altre linee del nostro Strumento risolver si possono; poiché, e quanti ne sono tra gli Elementi di Euclide, ed in molti altri autori, vengono da me con brevissime e facilissime maniere risoluti. Ma, come da principio si è detto, la mia presente intenzione è stata di parlar con persone militari solamente, e di pochissime altre cose fuori di quelle che a simili professori appartengono, riservandomi in altra occasione a publicare, insieme con la fabrica dello Strumento, una più ampla descrizione de' suoi usi.